Adicionar duas grandezas sinusoidais com a mesma frequência angular
Dadas duas grandezas sinusoidais descritas por:
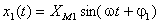 |
e |
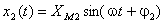 |
analiticamente, a sua soma será dada por:
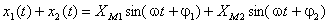
Se se representar cada grandeza pelo respectivo vector girante, a sua soma será representada pela soma dos dois vectores; a evolução temporal da soma corresponde à parte imaginária deste vector soma:
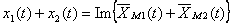
ANIMAÇÃO
Multiplicar uma grandeza sinusoidal por uma constante real
Dada a grandeza sinusoidal descrita por:
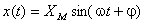
analiticamente, a sua multiplicação pela constante real 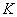 é dada por:
é dada por:
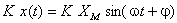
Se se representar a grandeza pelo respectivo vector girante, a sua multiplicação por 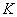 é representada por um vector colinear com
é representada por um vector colinear com 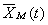 mas cujo módulo vale
mas cujo módulo vale 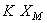 ; a evolução temporal
; a evolução temporal 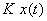 corresponde à parte imaginária deste vector:
corresponde à parte imaginária deste vector:
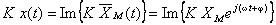
ANIMAÇÃO
Produto de duas grandezas sinusoidais com a mesma frequência angular
Dadas duas grandezas sinusoidais descritas por:
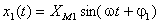 |
e |
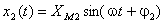 |
analiticamente, o seu produto será dado por:
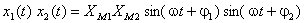
Se se representar cada grandeza pelo respectivo vector girante, o seu produto será representado por um vector de fase 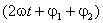 , isto é, rodará com uma frequência angular dupla, e de módulo
, isto é, rodará com uma frequência angular dupla, e de módulo 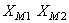 ; a evolução temporal do produto corresponde à parte imaginária deste vector:
; a evolução temporal do produto corresponde à parte imaginária deste vector:
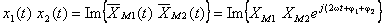
ANIMAÇÃO ????
Derivação de uma grandeza sinusoidal
Dadas a grandeza sinusoidal descrita por:
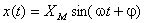
analiticamente, a sua derivada será dada por:
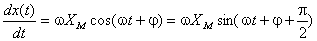
Se se representar a grandeza pelo respectivo vector girante, a sua derivada será representada por um vector de fase 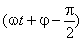 , isto é, avançado
, isto é, avançado  relativamente a
relativamente a 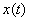 , e de módulo
, e de módulo 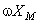 ; a evolução temporal da derivada corresponde à parte imaginária deste vector:
; a evolução temporal da derivada corresponde à parte imaginária deste vector:
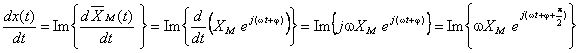
ANIMAÇÃO
Integração de uma grandeza sinusoidal
Dadas a grandeza sinusoidal descrita por:
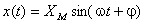
analiticamente, o seu integral será dado por:
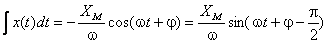
Se se representar a grandeza pelo respectivo vector girante, o seu integral será representado por um vector de fase 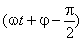 , isto é, atrasado
, isto é, atrasado  relativamente a
relativamente a 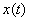 , e de módulo
, e de módulo 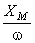 ; a evolução temporal do integral corresponde à parte imaginária deste vector:
; a evolução temporal do integral corresponde à parte imaginária deste vector:
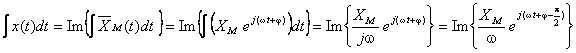
ANIMAÇÃO