La loi des mailles indique, qu'à tout instant, la somme algébrique des tensions le long d'une maille est nulle.

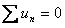
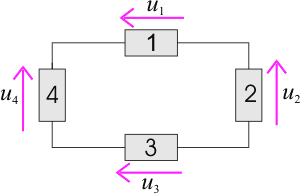
Figure 6 – Schéma représentatif de la Loi des Mailles

Compte tenu du sens de référence des tensions indiqué sur la Figure 6 et en additionnant les tensions dans le sens des aiguilles d'une montre, la loi des mailles permet d'écrire :

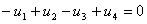
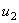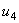On a considéré ici l'opposé des tensions e car leur sens de référence est à l'opposé du sens de circulation dans la maille. Le fait d'avoir choisi un sens de circulation anti-horlogique n'est cependant pas déterminant. si on avait choisi un sens horlogique on aurait obtenu une équation différente mais rigoureusement équivalente.

Figure 7 – Mailles du circuit

Dire que la comme des tensions le long d'une maille est nulle est équivalent à dire que le travail nécessaire pour déplacer une charge le long d'une maille est nul. En d'autres mots cela veut dire que le système est conservatif : le travail fourni par d'éventuelles sources présentes au sein de la maille pour déplacer une charge au sein de celle-ci est absorbé par les récepteurs présents au sein de cette même maille.

Pour le circuit de la Figure 7, l'application de la loi des mailles permet d'écrire :

• Pour la maille rouge et un sens de circulation anti-horlogique :
• Pour la maille bleue et un sens de circulation anti-horlogique :
• Pour la maille verte et un sens de circulation anti-horlogique :

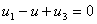
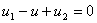
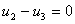
Parmi ces 3 équations, seulement 2 sont linéairement indépendantes.

S'il existe M mailles dans le circuit, la loi des mailles permet d'écrire 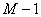équations linéairement indépendentes.

La dernière équations permet de dire que ma tensions aux bornes de l'élément 2 est égale à la tension aux bornes de l'élément 3 ; en d'autres mots, les deux éléments présentent la même tension à leurs bornes. Dans ce cas, on dit que les éléments sont connectés en parallèle.