Calcul de C, Q et U
Exemple de calcul de C, Q et U pour un circuit avec condensateurs en série et en parallèle
Reprenons l'exemple déjà vu pour la recherche du condensateur équivalent (revoir ici)
Soit UAB = 100 V
Si, en plus de devoir rechercher la capacité équivalente, on doit calculer C, U et Q des condensateurs individuels du circuit de départ, donnez un numéro aux circuits obtenus lors du processus de simplification.
Donc pour rappel, on a obtenu :
circuit 1 :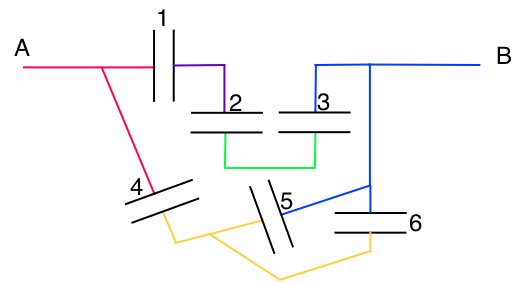 
avec tous les condensateurs de C = 1 μF
circuit 2 :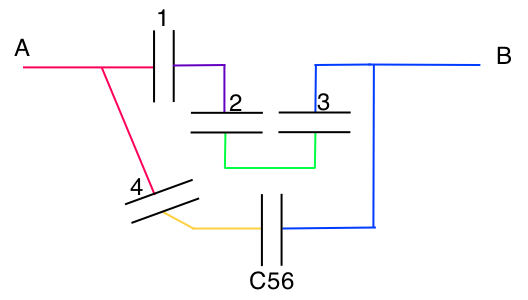 
avec C56 = 2 μF
circuit 3 :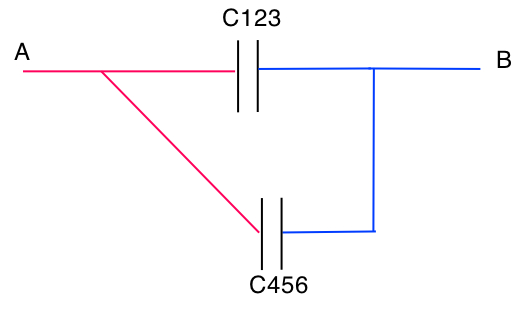 
avec C123 = (1/3) μF et C456 = (2/3) μF
circuit 4 :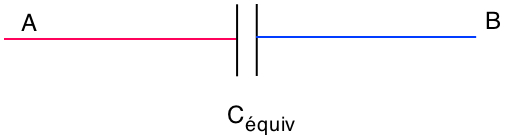 
avec Céquiv = 1 μF
On commence par le circuit 4.
- On connait : UAB = 100 V et C = Céquiv = 1 μF (calculé lors de la simplification)
- On calcule Q = C . U = 10-4 C
On remonte au circuit 3.
- On connait U123 = U456 = UAB = 100 V (en parallèle, même U) et C123 = (1/3) μF et C456 = (2/3) μF (calculés lors de la simplification)
- On calcule Q123 = C123 . U = (1/3) . 10-4 C et Q456 = C456 . U = (2/3) . 10-4 C
On remonte au circuit 2.
Branche du haut :
- On connait Q1 = Q2 = Q3 = Q123 = (1/3) . 10-4 C (en série, même Q) et C1 = C2 = C3 = 1 μF (données)
- On calcule \( \class{formule}{ U1 = \dfrac{Q1}{C1} = \dfrac{100}{3} V }\) ; \( \class{formule}{ U2 = \dfrac{Q2}{C} = \dfrac{100}{3} V }\) ; \( \class{formule}{ U3 = \dfrac{Q3}{C3} = \dfrac{100}{3} V }\)
Branche du bas :
- On connait Q4 = Q56 = Q456 = (2/3) . 10-4 C (en série, même Q) et C4 = 1 μF (données) et C56 = 2 μF (calculé lors de la simplification)
- On calcule \( \class{formule}{ U4 = \dfrac{Q4}{C4} = \dfrac{200}{3} V }\) ; \( \class{formule}{ U56 = \dfrac{Q56}{C56} = \dfrac{100}{3} V }\)
On remonte au circuit 1.
- On connait U5 = U6 = U56 (en parallèle, même U) et C5 = C6 = 1 μF (données)
- On calcule Q5 = C5 . U5 = (1/3) . 10-4 C ; Q6 = C6 . U6 = (1/3) . 10-4 C