Réfraction - dioptre plan

Prérequis

• la réfraction

Présentation

Ces deux animations montrent le passage d'un rayon lumineux d'un milieu à un autre, d'indice de réfraction différent, dans le cas d'un dioptre plan, et vous permettent de prendre des mesures des angles.

Première animation

Les indications de manipulation se trouvent sous l'animation.

auteur : Geneviève Tulloue, université de Nantes

Explications

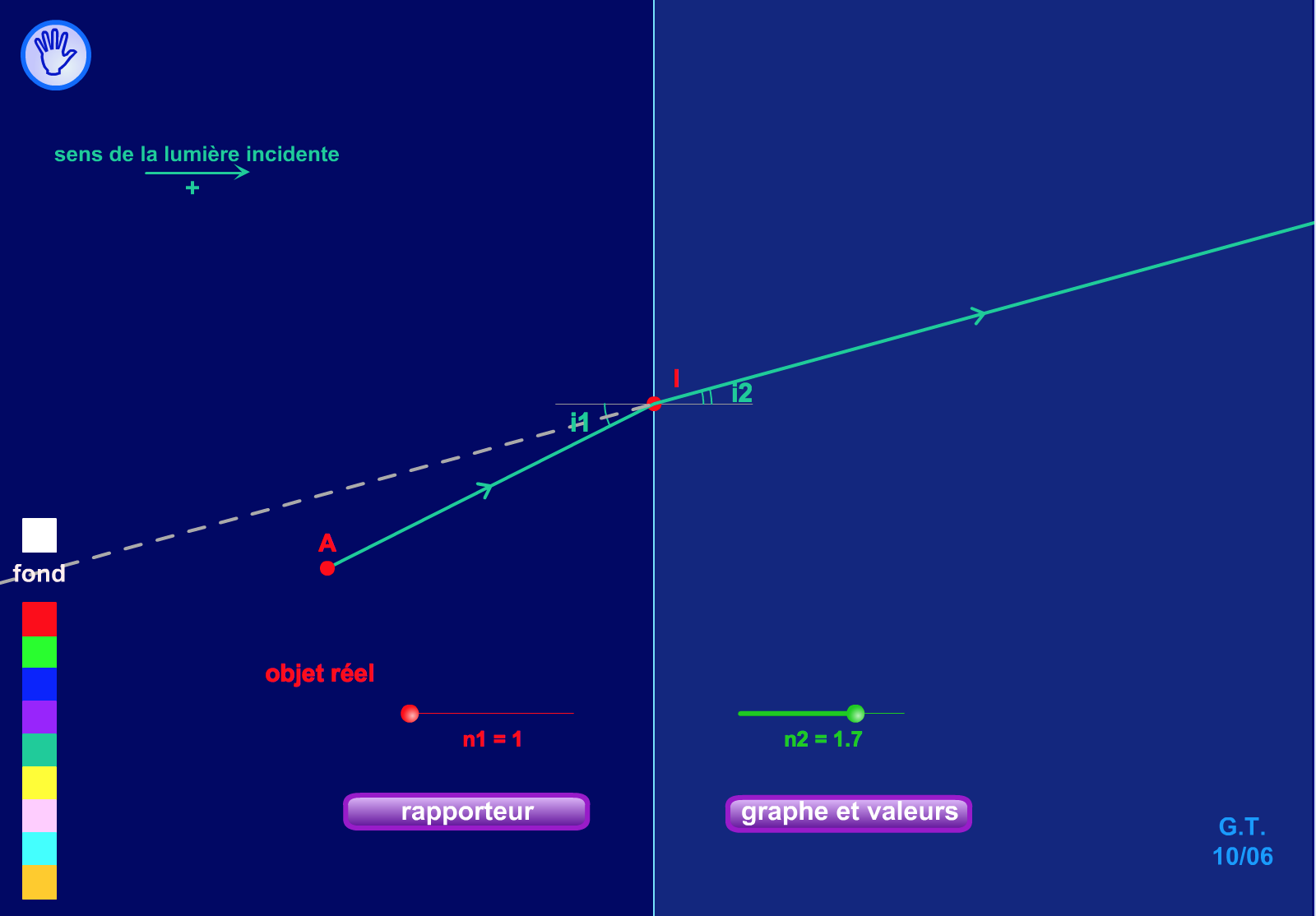
Lorsque vous lancez l'animation, vous voyez un rayon incident (partie de gauche) qui rencontre un changement de milieu (au centre).
L'angle d'incidence est appelé i1, et l'angle de réfraction est appelé i2 (attention, cela change de la notation de ce cours où les angles de réfraction sont notés r, à part dans le cas des prismes).
Cliquez sur le bouton "rapporteur" pour mieux visualiser les angles.

1. n1 < n2

   Au démarrage de l'animation, l'indice du milieu incident est égal à 1, et celui du milieu de réfraction est égal à 1,7 (donc n1 < n2).
   
   • Le rayon réfracté est-il toujours du même côté de la normale que le rayon incident ? Ou toujours de l'autre côté ? Vérifiez votre prédiction en déplaçant le rayon incident (cliquez et tirez sur le point rouge A).
   • Le rayon réfracté se rapproche-t-il ou s'éloigne-t-il de la normale ? Cela correspond-il à ce que vous pouvez prévoir sur base de la relation n1 . sin i1 = n2 . sin i2 ?
   • Sur base de cette relation, que vaudra i2 si le rayon incident est perpendiculaire au dioptre ? Vérifiez votre prédiction en déplaçant le rayon incident.
   • Pour ces mêmes valeurs des indices de réfraction, dessinez le graphe de sin i2 en fonction de sin i1. Vérifiez votre graphe en cliquant sur le bouton "graphe et valeurs".
     
   • Prenez ensuite une autre valeur pour i1 et calculez i2. Comparez votre résultat à celui indiqué.
   • Le rayon réfracté peut-il avoir un angle i2 quelconque ? Ou a-t-il une valeur minimum ou maximum (si oui, comment calculer ces valeurs) ? Vérifiez votre prédiction en déplaçant le rayon incident.
   • A présent, tout en gardant n1 = 1, changez la valeur de n2. Sur base de la relation n1 . sin i1 = n2 . sin i2 et/ou du graphe fait plus haut, répondez à la question suivante : si n2 augmente, la déviation sera-t-elle plus importante ou plus faible ? Vérifiez votre prédiction grâce à l'animation.

2. n1 > n2
   

   Augmentez ensuite n1, et diminuer n2 de façon à avoir n1 > n2.
   • Le rayon réfracté est-il toujours du même côté de la normale que le rayon incident ? Ou toujours de l'autre côté ? Vérifiez votre prédiction en déplaçant le rayon incident (cliquez et tirez sur le point rouge A). Quelle différence avec le cas précédent (n1 < n2) ?
   • Le rayon réfracté se rapproche-t-il ou s'éloigne-t-il de la normale ? Cela correspond-il à ce que vous pouvez prévoir sur base de la relation n1 . sin i1 = n2 . sin i2 ? Quelle différence avec le cas précédent (n1 < n2) ?
     
   • Sur base de cette relation, que vaudra i2 si le rayon incident est perpendiculaire au dioptre ? Vérifiez votre prédiction en déplaçant le rayon incident. Quelle différence avec le cas précédent (n1 < n2) ?
   • Pour ces mêmes valeurs des indices de réfraction, dessinez le graphe de sin i2 en fonction de sin i1. Vérifiez votre graphe en cliquant sur le bouton "graphe et valeurs". Quelle différence avec le cas précédent (n1 < n2) ?
   • Prenez ensuite une autre valeur pour i1 et calculez i2. Comparez votre résultat à celui indiqué.
   • Le rayon réfracté peut-il avoir un angle i2 quelconque ? Ou a-t-il une valeur minimum ou maximum (si oui, comment calculer ces valeurs) ? Vérifiez votre prédiction en déplaçant le rayon incident. Quelle différence avec le cas précédent (n1 < n2) ?
   • Il y a un angle d'incidence pour lequel i2 = 90°. Cet angle est appelé angle critique. Que se passe-t-il si i1 est supérieur à l'angle critique ?
   • Comment varie l'angle critique si n1 augmente ? Cherchez la réponse par formules et ensuite vérifiez-la à l'aide de l'animation.
     

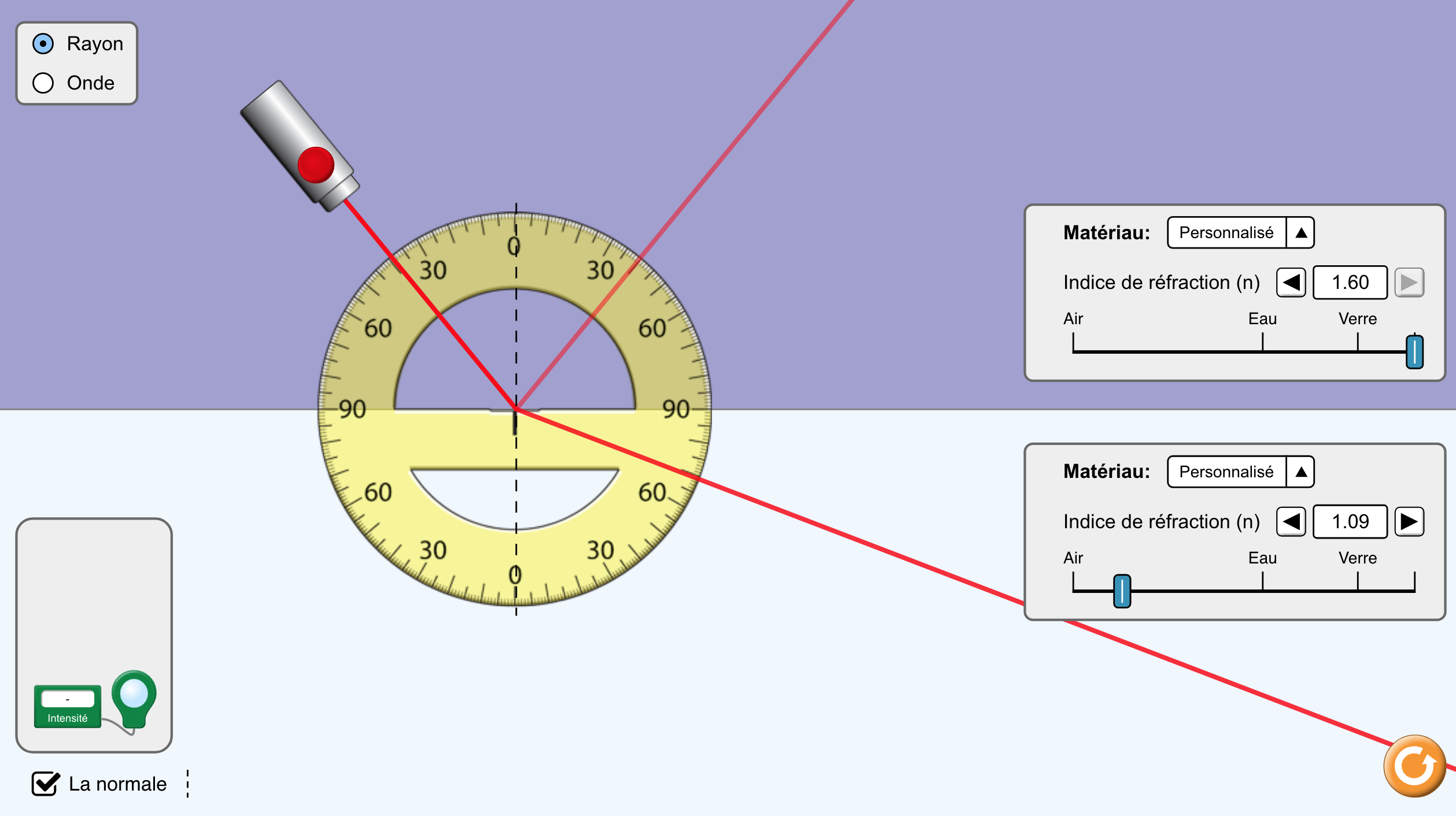
Seconde animation

Vous pouvez faire les mêmes observations avec cette autre animation dans laquelle vous sélectionnez "Intro".

auteur : Simulations interactives PhET à l'Université du Colorado Boulder