Vecteurs - produit vectoriel
Prérequis
Présentation
-
Commençons par observer cette animation simple. On y voit quelques situations particulières :
- les 2 vecteurs parallèles,
- les 2 vecteurs perpendiculaires,
- les 2 vecteurs antiparallèles,
- les 2 vecteurs perpendiculaires mais inversés par rapport au cas précédent.
Observez la norme et l'orientation du vecteur résultant de ce produit vectoriel.
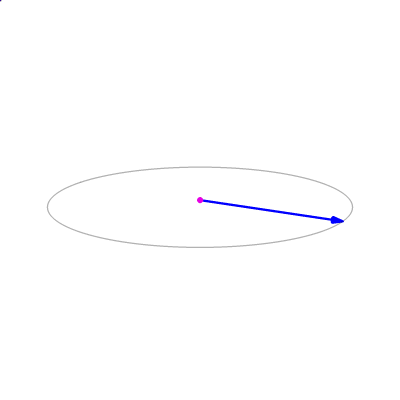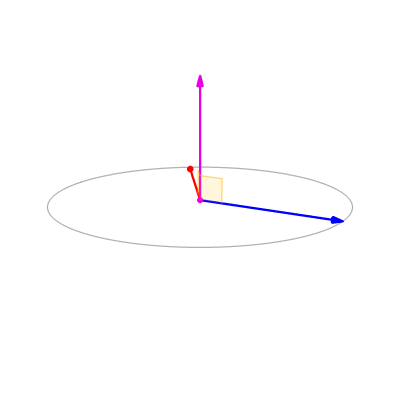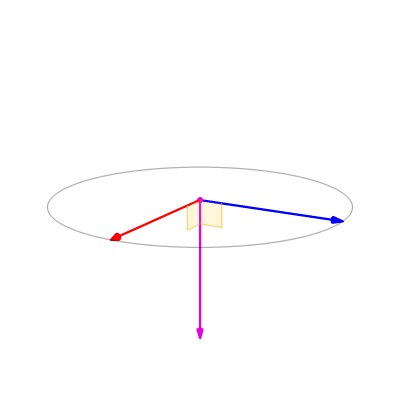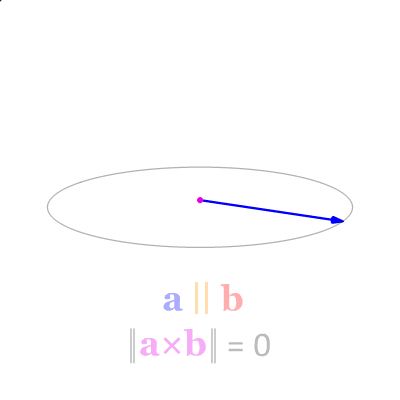
auteur: LucasVB (Travail personnel) [Public domain], via Wikimedia Commons
-
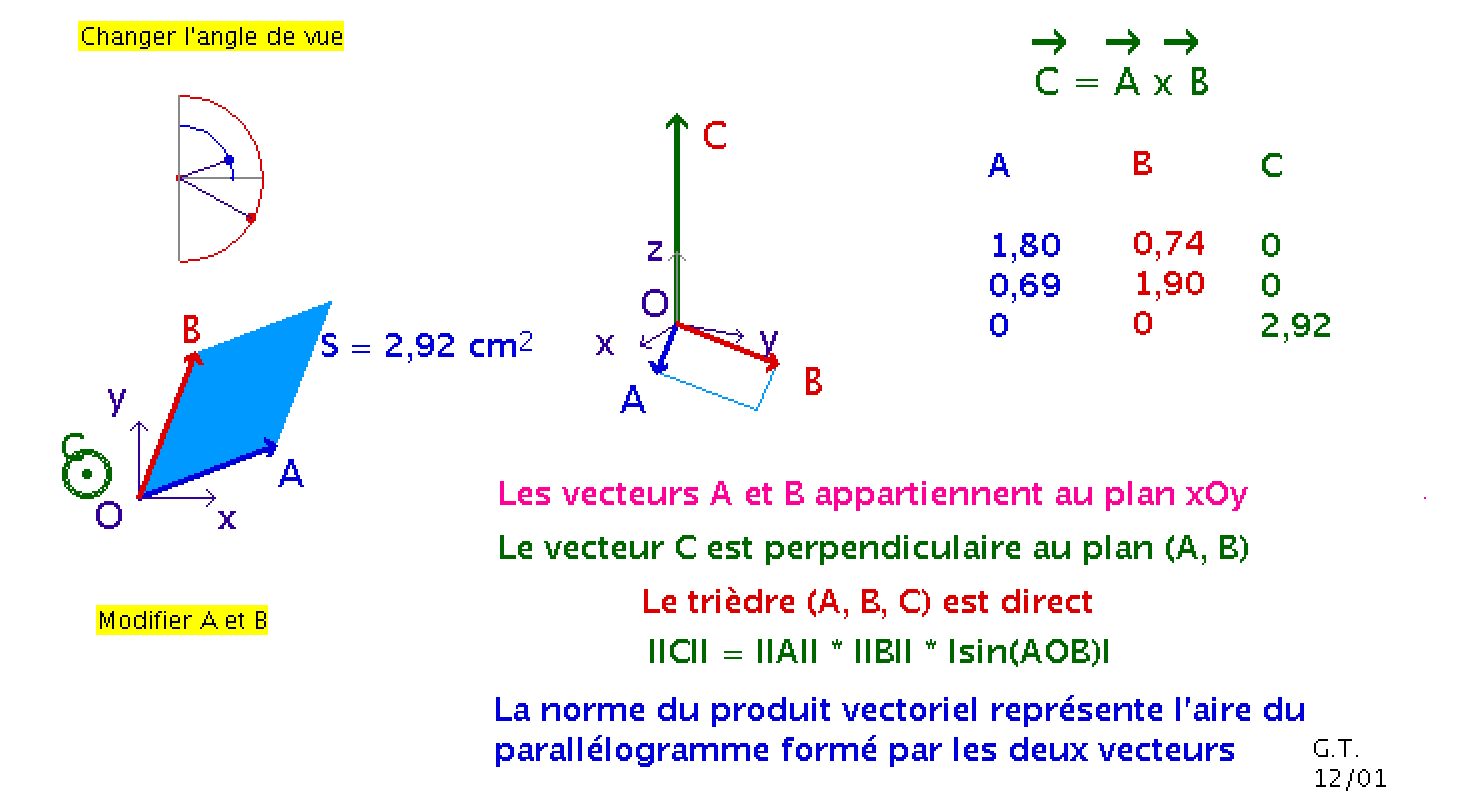
Passons ensuite au cas général, avec une animation interactive.
Cette animation peut être considérée comme un mini laboratoire. Observez, modifiez, réfléchissez.- Changez la norme des vecteurs £A et £B et observez comment change £C.
- Changez l'angle entre £A et £B et observez comment change £C.
- Permuttez £A et £B et observez comment change £C.
auteur : Geneviève Tulloue, université de Nantes
-
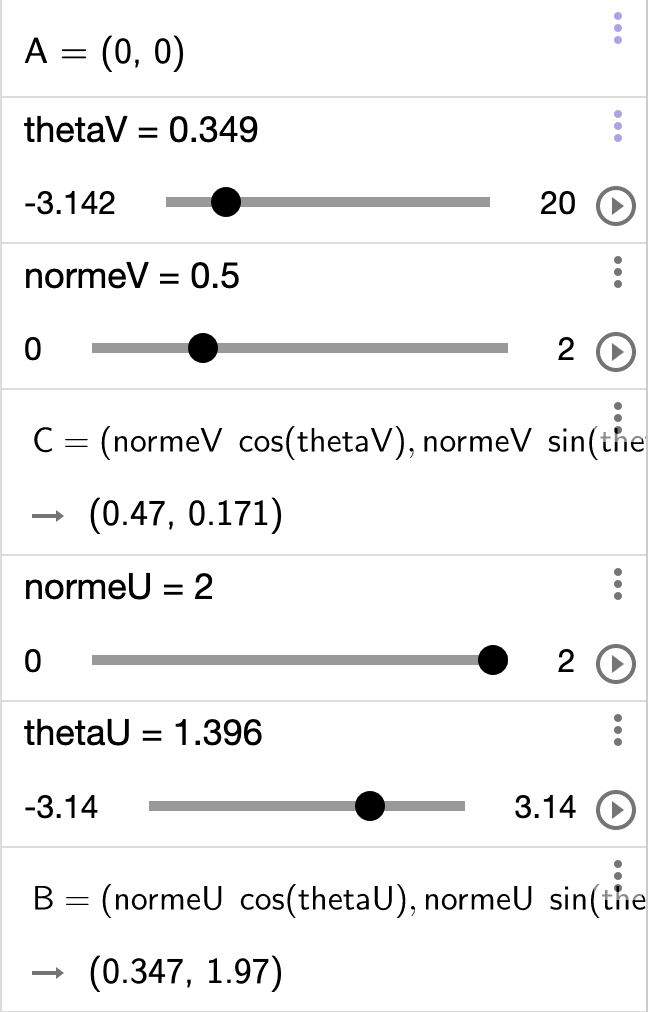
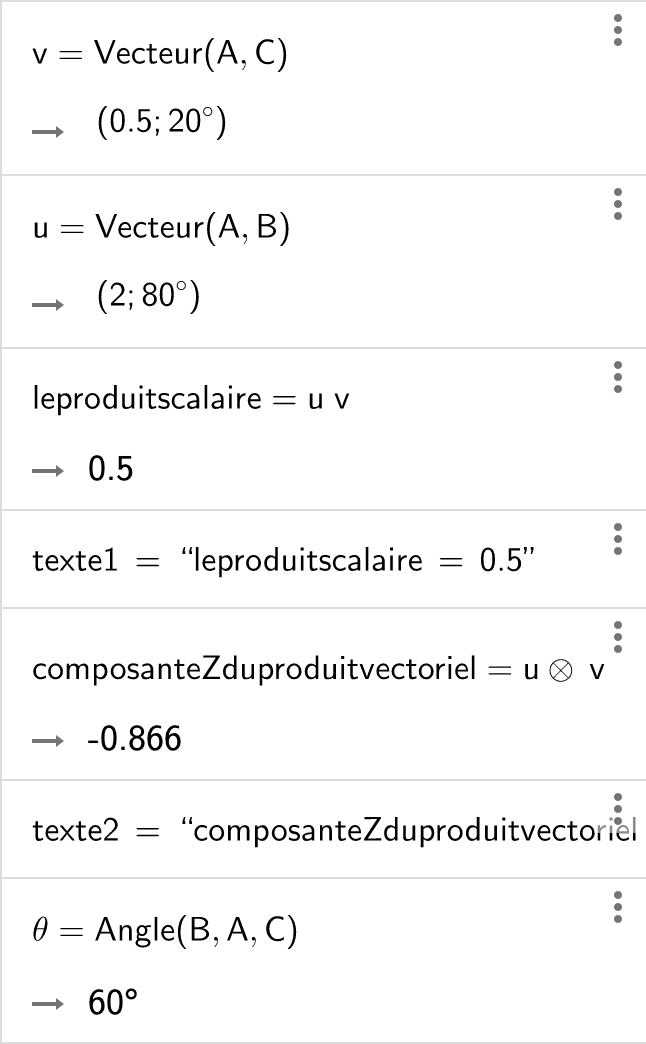
Terminons par une vidéo, dans laquelle vous voyez deux vecteurs u et v, avec, au départ, un angle de 60° entre eux. On voit ensuite la composante selon l'axe Z (vertical sortant de l'écran) du produit vectoriel. Que se passe-t-il si on double la norme d'un des deux vecteurs ? Ou si on la diminue de moitié ?
Que vaut le produit vectoriel quand l'angle vaut 0° ? 180° ? 270° (ou -90°) ?
Remettons un angle de 60°. Que se passe-t-il si on inverse les deux vecteurs ?Pour construire vous-même ces vecteurs et modifier leurs normes et leur orientation, utilisez GeoGebra (application ou version en ligne), en vous inspirant des éléments indiqués ci-dessous.