Procédures et fonctions en assembleur

Notre processeur peut être programmé en langage d’assemblage grâce aux multiples instructions qu’il supporte. En théorie, ce langage d’assemblage est suffisant pour écrire n’importe quel programme. Cependant, il est fastidieux et dangereux d’écrire un programme sans le découper en fonctions et procédures qui peuvent être testées indépendamment et qui sont ensuite combinées.

Vous avez utilisé des fonctions et procédures dans le langage python sans analyser en détails comment ce langage supportait ces différentes constructions. Nous allons maintenant les analyser en nous appuyant sur le langage d’assemblage de notre processeur.

Commençons par réfléchir aux différentes opérations qu’un langage de programmation tel que python doit réaliser pour supporter différents types de fonctions. Tout d’abord, analysons comment implémenter une procédure, c’est-à-dire une fonction qui ne prend pas d’argument et ne retourne pas de résultat. Notre premier exemple simple est une procédure qui affiche de l’information à l’écran. Une telle procédure pourrait être utilisée dans un programme pour afficher le contenu d’un menu à l’écran.

def p():
    print("Bonjour")

Il est intéressant d’analyser comment un langage tel que python fait appel à une telle procédure dans un programme.

Regardons plus en détails le code ci-dessous. La première ligne initialise la variable x à la valeur 1. La deuxième ligne transfère l’exécution du programme à la procédure p(). Le code de cette procédure est composé d’un ensemble d’instructions qui se trouvent en mémoire et vont afficher Bonjour à l’écran. Après l’exécution de cette procédure, le programme python retourne à l’exécution de la troisième ligne et place la valeur 2 dans la variable x. La quatrième ligne relance l’exécution de la procédure p(). Celle-ci va à nouveau exécuter les instructions qui permettent d’afficher Bonjour à l’écran, mais après son exécution le programme python exécutera la ligne 5. On remarque une différence importante entre les deux invocations de la procédure p(). Après la première invocation, on exécute la ligne 3 du programme python. Après la deuxième invocation, on exécute la ligne 5 du programme python.

x=1            # ligne 1
p()            # ligne 2
x=2            # ligne 3
p()            # ligne 4
x=3            # ligne 5

En python, il est facile d’imprimer de l’information à l’écran. En assembleur, cette opération nécessite nettement plus d’efforts. Analysons un autre exemple en python qui utilise les variables globales. En python, une fonction utilise normalement les arguments qu’elle a reçu ou définit ses propres variables locales. Il est aussi possible de définir des variables globales, c’est-à-dire des variables qui sont stockées dans la mémoire du programme et sont accessibles à toutes les fonctions de ce programme. Cette utilisation d’une variable globale est illustrée dans le programme python ci-dessous.

compteur=0

def compte():
    global compteur
    compteur = compteur+1

x=1          # ligne 1
compte()     # ligne 2
x=2          # ligne 3
compte()     # ligne 4
x=3          # ligne 5

La variable compteur est une variable globale (python impose l’utilisation du mot clé global dans sa définition dans la procédure compte) qui est initialisée dans le programme principal et modifiée dans la procédure compte. Analysons l’exécution de ce programme pas à pas. Ce programme manipule deux variables en mémoire : x et compteur. La première ligne initialise la variable x à la valeur 1. La deuxième ligne incrémente la variable compteur qui passe à 1. La troisième ligne fait passer la valeur de la variable x à 2. La quatrième ligne incrémente la variable compteur qui passe également à 2. Enfin, la dernière ligne place la valeur 3 dans la variable x.

Pour bien comprendre comment une telle procédure peut être utilisée à plusieurs endroits dans un même programme, il est intéressant d’essayer de la convertir en minuscule assembleur.

Commençons par assigner une zone mémoire pour la variable x. Nous pouvons ensuite écrire en assembleur les lignes impaires qui correspondent aux différentes assignations de cette variable.

          JMP start
x:        DB 0
compteur: DB 0
start:
          MOV x, 1  ; ligne 1
          ; à compléter
          MOV x, 2  ; ligne 3
          ; à compléter
          MOV x, 3  ; ligne 5

Nous devons également assigner une zone mémoire pour stocker la variable compteur. Supposons que celle-ci soit stockée aux adresses 16 et 17. La Fig. 13 présente le contenu initial de notre mémoire.

Fig. 13 Contenu initial de la mémoire

Il nous faut maintenant pouvoir faire appel à la procédure compte() après l’exécution des lignes 1 et 3. Le corps de cette procédure peut s’écrire en trois instructions en assembleur.

MOV A, [compteur]
INC A
MOV compteur, A

L’exemple ci-dessus utilise le registre A, mais il aurait pu aussi être écrit avec n’importe lequel des trois autres registres.

Une première approche pour inclure notre procédure dans le programme en minuscule assembleur est d’intégrer directement ces instructions en ligne (inline en anglais). Cette technique est parfois utilisée dans certains langages de programmation pour de très petites fonctions qui doivent s’exécuter rapidement. Elle revient à copier-coller le code de la procédure dans le programme.

          JMP start
x:        DB 0
compteur: DB 0
start:
          ; ligne 1
          MOV x, 1
          ; copie du code de la procédure
          MOV A, [compteur]
          INC A
          MOV compteur, A
          ; ligne 3
          MOV x, 2
          ; copie du code de la procédure
          MOV A, [compteur]
          INC A
          MOV compteur, A
          ; ligne 5
          MOV x, 3

Cette approche fonctionne dans notre exemple simple, mais elle a deux inconvénients majeurs. Le premier est que le code de la procédure doit être recopié à chaque invocation de la procédure dans un programme. Cela consomme inutilement de l’espace mémoire surtout si le programme appelle la procédure à de nombreux endroits. Le deuxième inconvénient est que si la procédure modifie le contenu d’un registre, elle pourrait avoir un impact non-voulu sur les instructions du programme principal. Dans notre cas, si nous utilisions le registre A dans le code qui se trouve entre les appels à la procédure p, cette valeur serait écrasée par le code de la procédure et notre programme serait en erreur.

Il est nécessaire de pouvoir isoler les instructions de la procédure dans une partie de la mémoire et d’y faire appel en exécutant un saut inconditionnel. Une première approche pourrait être la suivante. La code de la procédure compte est placé après l’étiquette COMPTE et on fait appel à la procédure en utilisant un saut inconditionnel vers cette adresse.

          JMP start
x:        DB 0
compteur: DB 0
start:
          ; ligne 1
          JMP COMPTE
ligne3:   ; ligne 3
          MOV x, 2
          JMP COMPTE
ligne5:   ; ligne 5
          MOV x, 3

COMPTE:
          MOV A, [compteur]
          INC A
          MOV compteur, A
          JMP retour

Malheureusement, ce n’est pas suffisant. Après la première exécution de la procédure compte, l’exécution doit reprendre à l’adresse ligne3 tandis qu’après la seconde exécution de la même procédure, il faut poursuivre l’exécution du programme principal à partir de l’adresse ligne5. Pour résoudre ce problème, nous devons rendre le code de la procédure plus générique. Notre procédure doit pouvoir retourner à l’adresse qui suit celle à partir de laquelle elle a été appelée. Dans notre assembleur, comme dans la plupart des assembleurs, cela se fait en utilisant deux instructions spéciales: CALL pour appeler une procédure et RET pour terminer l’exécution d’une procédure et retourner à l’adresse qui suit celle de l’appel. Cette adresse est appelée l”adresse de retour. L’instruction CALL la sauvegarde en mémoire et ensuite fait un saut à l’adresse qui est son unique argument. L’exécution d’une procédure se déroule comme suit:

1. Sauvegarde de l’adresse de retour en mémoire

2. Appel de la procédure (via l’instruction JMP)

3. Exécution du corps de la procédure

4. Récupération de l’adresse de retour

5. Saut à l’adresse de retour pour poursuivre l’exécution du programme appelant

Les deux premières opérations sont exécutées par l’instruction CALL. Les deux dernières sont exécutées par l’instruction RET.

Il est intéressant de voir comment le simulateur exécute l’instruction CALL. Pour cela, considérons le minuscule programme ci-dessous:

JMP start
fonction:
    RET
start:
    CALL fonction

La Fig. 14 présente l’état de la mémoire avant l’exécution de l’instruction CALL. La Fig. 15 montre que la pile est vide à ce moment. Le registre SP contient l’adresse 0x39C comme sommet de pile/

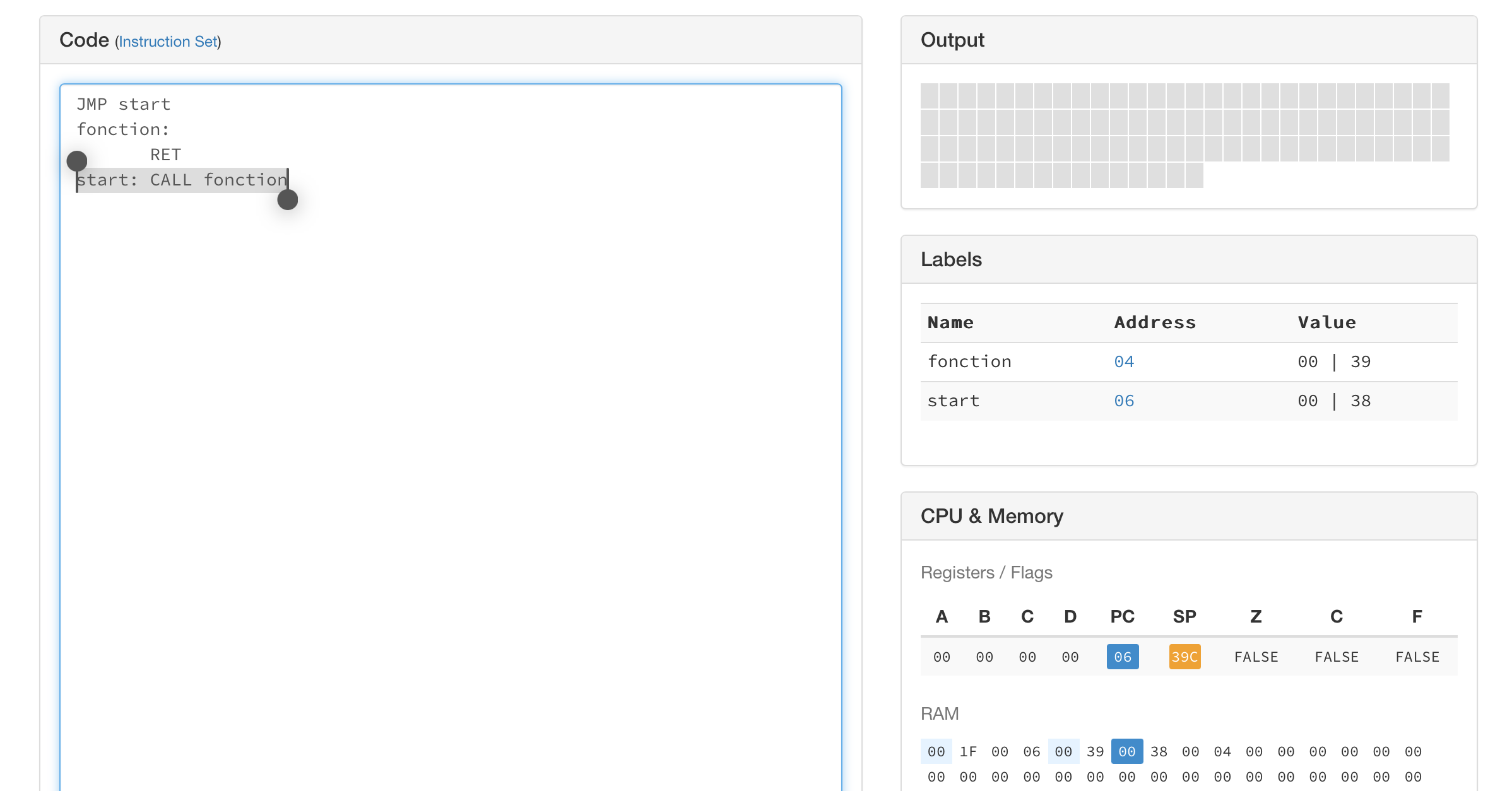
Fig. 14 Etat de la mémoire avant l’exécution de l’instruction CALL

Fig. 15 Etat de la pile avant l’exécution de l’instruction CALL

L’instruction CALL se trouve à l’adresse 0x06. En mémoire, cette instruction occupe deux blocs de 16 bits. L’instruction suivante se trouve donc à l’adresse 0x0A. La Fig. 16 présente l’état de la mémoire après l’exécution de l’instruction CALL. On remarque que le sommet de la pile se trouve maintenant à l’adresse 0x39A. La Fig. 17 montre que la pile contient bien l’adresse de retour (0x0A).

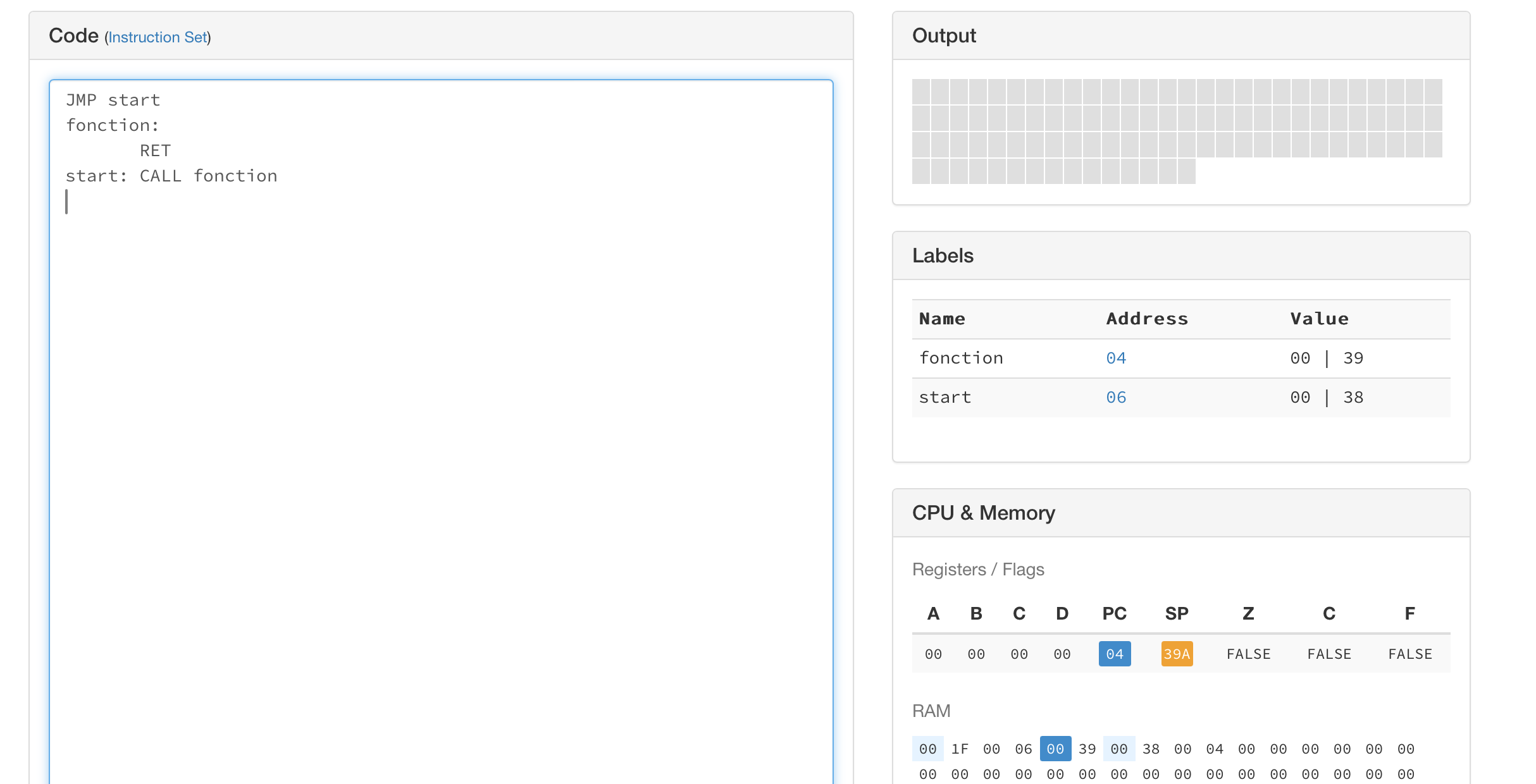
Fig. 16 Etat de la mémoire après l’exécution de l’instruction CALL

Fig. 17 Etat de la pile après l’exécution de l’instruction CALL

Grâce à l’instruction CALL, notre programme devient donc :

           JMP start
x:         DB 0
compteur:  DB 0
; ligne 1
start:
           CALL COMPTE
ligne3:                ; ligne 3
           MOV x, 2
           CALL COMPTE
ligne5:                ; ligne 5
           MOV x, 3

COMPTE:
           MOV A, [compteur]
           INC A
           MOV compteur, A
           RET

Il est intéressant d’observer l’évolution du processeur et de la mémoire durant l’exécution de ce programme. L’exécution de la première l’instruction CALL COMPTE a trois effets sur le processeur et la mémoire. Après exécution de l’instruction, le compteur de programme pointe vers l’adresse de l’étiquette COMPTE afin de pouvoir exécuter la première instruction de la procédure. L’exécution de l’instruction CALL modifie également le registre SP (Stack Pointer en anglais). Au démarrage du processeur, ce registre contient la valeur 39C qui correspond à une adresse dans la partie « haute » de notre mémoire. Après l’exécution de l’instruction CALL, la valeur stockée dans le registre SP a été réduite de deux unités et est passé à la valeur 39A. Si l’on observe la mémoire à l’adresse 39C, on remarque que l’instruction CALL y a placé l’adresse de retour de la procédure, c’est-à-dire celle de l’étiquette ligne3 dans notre exemple.

Le code de la procédure s’exécute et se termine par l’instruction RET. Celle-ci a également trois effets comme l’instruction CALL. Tout d’abord, elle lit en mémoire la valeur qui se trouve à l’adresse stockée dans le registre SP. Cette valeur est l’adresse qu’il faut placer dans le compteur de programme pour retourner à l’adresse qui suit celle de l’appel de la procédure (l’étiquette ligne3 dans notre exemple). L’instruction RET modifie également la valeur stockée dans le registre SP en l’incrémentant de deux unités.

Le registre SP n’est pas utilisé par les instructions habituelles telles que MOV ou ADD. Il ne sert que pour les instructions CALL et RET. Grâce à ce registre, il est possible de maintenir en mémoire une structure de données appelée une pile (ou stack en anglais). Une pile est une structure de données permettant de stocker un nombre quelconque de données. Elle supporte deux opérations: l’ajout d’une donnée au sommet de la pile (push en anglais) et le retrait de la donnée se trouvant au sommet de la pile (pop en anglais). La pile de notre processeur est stockée en mémoire et à tout moment l’adresse du sommet de la pile se trouve dans le registre SP.

La pile la plus connue dans la vie de tous les jours est la pile d’assiettes. Lorsque l’on a besoin d’un assiette, on prend celle qui se trouve au sommet de la pile. Après avoir fait la vaisselle, on remet les assiettes propres au sommet de la pile également. Pour bien comprendre le fonctionnement d’une structure de données en pile en informatique, il suffit de se rappeler comment on manipule une pile d’assiettes…

Note

Comment stocker une pile de mots en mémoire ?

La solution la plus simple pour stocker et manipuler une pile de mots en minuscule assembleur est d’utiliser une zone de mémoire contiguë. Une première approche serait d’utiliser l’adresse p pour stocker l’élément se trouvant en bas de la pile et d’ajouter les éléments suivants aux adresses p+2, p+4, … Pour illustrer cette approche, la Fig. 18 présente l’évolution d’une pile initialement vide lors de l’exécution de la séquence push(3) ; pop ; push(2) ; push(5) d’opérations. Avec cette approche, le sommet de la pile est toujours l’élément dont l’adresse est numériquement la plus élevée.

Fig. 18 Évolution de la pile vers les adresses numériquement croissantes

Outre les données, une telle structure doit également stocker l’adresse de l’élément se trouvant au sommet de la pile. Après l’opération push(3) le sommet de la pile est à l’adresse p. Il est à la même adresse après l’opération push(2) et atteint l’adresse p+2 après l’opération push(5).

Une seconde approche est d’utiliser l’adresse p pour stocker le premier élément de la pile et d’ajouter les éléments suivants aux adresses p-2, p-4, … La Fig. 19 illustre l’évolution d’un telle pile lors de l’exécution des opérations suivantes: push(3) ; pop ; push(2) ; push(5). Avec cette approche, l’élément se trouvant au sommet de la pile est celui dont l’adresse est numériquement la plus basse.

Fig. 19 Évolution de la pile vers les adresses numériquement décroissantes

Outre les données, cette structure doit également stocker l’adresse de l’élément se trouvant au sommet de la pile. Après l’opération push(3) le sommet de la pile est à l’adresse p. Il est à la même adresse après l’opération push(2) et atteint l’adresse p-2 après l’opération push(5).

Même si la première solution peut paraître la plus naturelle par analogie aux piles d’assiettes, c’est généralement la deuxième solution qui est préférée car elle facilite la gestion de la mémoire et maximise l’espace qui est disponible pour la pile sans inutilement contraindre la mémoire utilisée par un programme. C’est ce que notre assembleur fait pour les instructions CALL et RET.

Notre assembleur supporte également les instructions PUSH et POP . L’instruction PUSH peut prendre trois types différents d’arguments:

• un identifiant de registre

• une adresse

• une constante

L’instruction POP ne prend qu’un seul argument, un identifiant de registre. A titre d’exemple, observons l’exécution du code assembleur ci-dessous:

PUSH 7
MOV 122, 3
PUSH [122]
MOV A, 4
PUSH A
POP B
POP C
POP D

La première instructions, PUSH 7 place la valeur 7 au sommet de la pile. La deuxième place la valeur 3 en mémoire à l’adresse 122. La troisième instruction place la valeur qui se trouve à l’adresse 122, c’est-à-dire 3 au sommet de la pile. La quatrième instruction, MOV A, 4 place la valeur 4 dans le registre A. La cinquième instruction sauve le contenu du registre A sur la pile. La figure Fig. 20 présente l’état de la pile à ce moment. Dans cette figure, sp est l’adresse qui se trouve dans le registre SP.

Fig. 20 État de la pile après l’exécution des trois instructions ``PUSH``.

La première instruction POP place la valeur qui est actuellement au sommet de la pile (c’est-à-dire 4) dans le registre B Elle décrémente ensuite le pointeur de sommet de pile de deux unités. La deuxième instruction POP stocke la valeur 3 dans le registre C. La figure Fig. 21 présente l’état de la pile en mémoire à cet instant.

Fig. 21 État de la pile après l’exécution de deux instructions ``POP``.

La troisième instruction POP retournera la valeur 7 dans le registre D et le registre SP contiendra l’adresse du sommet de la mémoire. Si on tente d’exécuter une instruction POP à ce moment, le processeur affichera Stack underflow comme message d’erreur indiquant que la pile est vide.

Durant son exécution, la mémoire d’un de nos programmes en assembleur comprendra trois parties. Le bas de la mémoire nous servira à stocker les données, variables et constantes dont le programme a besoin. Le haut de la mémoire servira lui à stocker la pile. Celle-ci démarre à une adresse haute et grandit vers le bas au fur et à mesure que l’on y stocke des adresses et des données. Nous verrons que cette pile a de nombreuses utilisations en assembleur et par extension dans les langages de programmation. Les instructions du programme se trouveront au milieu entre les données et la pile. Cette organisation de la mémoire est illustrée en Fig. 22.

Fig. 22 Organisation de la mémoire d’un programme en assembleur

La pile est utilisée par l’instruction CALL pour stocker l’adresse de retour. A la fin de l’exécution de la procédure, l’instruction RET la récupère. Ce n’est pas la seule utilisation de la pile. Celle-ci permet aussi de stocker des données de façon temporaire. Imaginons que notre procédure compte est utilisée dans le programme suivant.

           JMP start
x:         DB 0
compteur:  DB 0
start:     MOV A, 123
           CALL COMPTE
           ADD A, [compteur]
           MOV x, A
           HLT
COMPTE:
           MOV A, [compteur]
           INC A
           MOV compteur, A
           RET

Ce programme est équivalent au code python suivant qui lors de son exécution place la valeur 124 dans la variable x.

compteur=0

def compte():
   global compteur
   compteur = compteur+1

x=0
compte()
x=123+compteur

Si on exécute le programme équivalent en assembleur, on observe qu’à la fin de son exécution la variable x contient la valeur 2. En observant le code assembleur, on peut facilement comprendre la raison de cette erreur. Avant l’instruction CALL COMPTE, nous avons placé la valeur 123 dans le registre A. Malheureusement, la procédure compte utilise le registre A et met sa valeur à 1 lors de l’incrémentation de la variable compteur. Cette utilisation du registre A par la procédure est un problème. D’un côté, une procédure doit pouvoir modifier des valeurs de registres pour réaliser des calculs. D’un autre côté, le programme qui appelle la procédure ne peut pas savoir quels registres vont être utilisés par la procédure.

On peut résoudre ce problème de deux façons en utilisant la pile. La première solution est de forcer le programme appelant à sauver les valeurs des quatre registres sur la pile avant d’exécuter CALL et de récupérer les valeurs des quatre registres sur la pile dès le retour de la procédure. Dans notre exemple, cela pourrait se faire comme suit:

           JMP start
x:         DB 0
compteur:  DB 0
start:     MOV A, 123
           PUSH A
           PUSH B
           PUSH C
           PUSH D
           CALL COMPTE
           POP D
           POP C
           POP B
           POP A
           ADD A, [compteur]
           MOV x, A
           HLT
COMPTE:
           MOV A, [compteur]
           INC A
           MOV compteur, A
           RET

Lorsque l’on exécute ce programme, la variable x contient bien la valeur 124 comme en python. Notez l’ordre dans lequel les valeurs des registres sont stockées (A puis B puis C puis D) et ensuite récupérées sur la pile (D puis C puis B puis A). L’ordre dans lequel on pousse les valeurs sur la pile importe peut, pour autant qu’elles soient récupérées dans l’ordre exactement inverse.

Cette approche fonctionne, mais elle implique parfois des instructions inutiles. Dans notre exemple, la procédure compte n’utilise que le registre A. Il est donc inutile de sauver les valeurs stockées dans les trois autres registres, mais le programme appelant ne connaît pas cette caractéristique de notre procédure. Une meilleure approche est de laisser à la procédure appelée la responsabilité de préserver les valeurs des registres qu’elle modifie. C’est cette approche que nous utilisons dans l’exemple suivant.

           JMP start
x:         DB 0
compteur:  DB 0
start:     MOV A, 123
           CALL COMPTE
           ADD A, [compteur]
           MOV x, A
           HLT
COMPTE:
           PUSH A ; sauvegarde du contenu du registre A qui va être modifié
           MOV A, [compteur]
           INC A
           MOV compteur, A
           POP A  ; récupération du contenu du registre A
           RET

Dans ce programme, la procédure compte sauve la valeur du registre A sur la pile avant de la modifier. En pratique, le code d’une procédure commencera généralement par une sauvegarde des valeurs de registres qui peuvent être modifiés dans le corps de la procédure. Elle se terminera par les instructions POP correspondantes dans l’ordre inverse de celui utilisé pour stocker les données au début de la procédure.

Grâce à la pile, il est possible d’écrire des programmes qui contiennent un nombre quelconque de procédures qui s’appellent l’une l’autre et dans un ordre quelconque. La pile grandira au fur et à mesure des appels successifs à des procédures et rétrécira chaque fois qu’une procédure se termine. Il est important de noter que pour que ce système fonctionne correctement il est nécessaire que chaque procédure manipule correctement la pile. Si le sommet de la pile se situe à l’adresse z au début de l’exécution d’une procédure, à la fin de celle-ci la pile doit contenir exactement les mêmes informations. Si une procédure laissait la pile avec un élément en plus ou un élément en moins lorsqu’elle retourne à l’adresse de retour dans le programme appelant, alors le programme complet ne fonctionnerait plus correctement. Il faut être très rigoureux lorsque l’on écrit des programmes en langage assembleur qui manipulent la pile.

Note

Stack overflow

Les langages de programmation tels que python utilisent aussi une pile pour supporter les appels de procédures et de fonctions. C’est à l’interpréteur ou au compilateur de gérer correctement la pile. En général, le langage de programmation réserve une zone mémoire pour stocker la pile du programme. Certains langages de programmation comme python ou Java vérifient que la pile ne déborde pas lors de l’exécution d’un programme. Le cas échéant, ils lancent une exception qui indique un dépassement de pile (stack overflow en anglais) et le programme est arrêté. Pour cela, ils doivent vérifier l’état de la pile avant chaque opération push ou pop. D’autres langages de programmation comme le C ne vérifient pas la taille de la pile à chaque opération. Avec ces langages, il est possible que la pile croisse tellement qu’elle rencontre la zone contenant les instructions ou même les données du programme. Dans ce cas, le programme aura un comportement totalement incohérent. Certains problèmes de sécurité sur des programmes écrits en C exploitent ce genre de limitations du langage.

Nous avons utilisé la pile pour stocker les adresses de retour des procédures ainsi que pour sauvegarder temporairement les valeurs des registres. Ce n’est pas la seule utilisation de la pille. Elle va également nous permettre de supporter les fonctions auxquelles il faut passer des arguments du programme appelant vers la fonction, mais aussi récupérer des valeurs de retour. Il faut aussi permettre à une fonction d’utiliser de la mémoire pour stocker des données temporaires pendant son exécution et de libérer correctement cette mémoire après.

Revenons à un exemple simple en python pour bien comprendre les différences entre une fonction et une procédure. Notre première fonction, f1, prend un entier en argument et retourne un entier également. Durant son exécution, elle utilise une variable locale, y. La deuxième fonction, f2 prend également un entier en argument et retourne un résultat entier. Le corps de la fonction f2 fait deux appels à la fonction f1 et utilise deux variables locales. Enfin, la fonction min prend deux arguments entiers et retourne un résultat entier. Elle utilise également une variable locale.

# incrémente son argument de 1
def f1(x):
    y=x+1
    return(y)

# incrémente son argument de 2
def f2(x):
    y=f1(x)
    z=f1(y)
    return(z)

# retourne le minimum
def min(x,y):
    if (x<y):
        r=x
    else:
        r=y
    return(r)

print(f1(3)) # affiche 4
print(f2(5)) # affiche 7
print(min(3,5)) # affiche 3

Pour supporter ces différents types de fonctions, nous devons répondre à trois questions :

1. Comment un programme appelant peut-il passer les arguments à une fonction ?

2. Comment un programme appelant peut-il récupérer le résultat d’une fonction ?

3. Comment une fonction peut-elle utiliser de la mémoire pour stocker ses variables locales ?

Commençons par la première question. Avant d’appeler une fonction, il est nécessaire d’avoir d’abord calculé les valeurs des arguments que l’on doit passer à cette fonction. Une fonction peut avoir un, deux, ou un nombre quelconque d’arguments. Ceux-ci devront être placés à un endroit où la fonction pourra les récupérer. Dans notre processeur, ces arguments peuvent être mis à deux endroits différents:

• dans des registres, avec un argument par registre

• en mémoire

La première solution a l’avantage d’être simple et rapide. Il suffit d’exécuter une instruction MOV pour placer la valeur d’un argument au bon endroit. Malheureusement, notre processeur ne dispose que de quatre registres au total. Nous ne pourrons donc jamais supporter de fonction avec plus de quatre arguments.

La seconde solution est plus générale. Nous utilisons déjà la pile pour récupérer l’adresse de retour et on peut facilement envisager de placer des arguments sur la pile avant l’exécution d’une fonction. Il suffit pour cela d’utiliser l’instruction PUSH pour chaque argument à pousser sur la pile. La fonction pourra récupérer chaque argument en faisant appel à POP dans l’ordre inverse de celui du programme appelant.

Pour le résultat de la fonction, deux approches sont possibles. La première est d’utiliser la pile pour retourner ce résultat. La seconde est de placer le résultat de la fonction dans un registre du processeur. La première solution a l’avantage de permettre à une fonction de retourner plusieurs résultats, comme en python par exemple. La seconde est utilisée par de très nombreux langages de programmation. C’est celle que nous adoptons dans ce chapitre. Dans le cadre de ce syllabus, nous prenons la convention qu’une fonction écrite en assembleur retournera un seul mot de 16 bits et que ce résultat sera toujours placé dans le registre ``A``.

Pour que les fonctions et procédures écrites par un ou une informaticienne soient utilisables sans difficultés par d’autres personnes, il est important que le programme appelant et la fonction/procédure utilisent les mêmes conventions d’utilisation de la pile. Dans le cadre de ce syllabus, nous prenons les conventions suivantes pour les fonctions et procédures en assembleur :

• le premier argument d’une fonction/procédure est toujours placé dans le registre ``D``.

• les deuxième, troisième, … arguments d’une fonction/procédure sont poussés sur la pile par le programme appelant avec la séquence d’instructions ``PUSH arg2``, ``PUSH arg3``, … avant l’instruction ``CALL``.

• le résultat ou valeur de retour d’une fonction est toujours placée dans le registre ``A``

• lors de l’appel à une fonction/procédure, le programme appelant a la garantie que les registres ``B`` et ``C`` auront la même valeur au retour de la fonction/procédure qu’avant l’appel. Cela implique que le programme appelant ne doit pas sauver ces registres sur la pile avant d’appeler une fonction/procédure. Par contre, si la fonction/procédure utilise les registres ``B`` ou ``C``, elle doit préserver leurs valeurs en utilisant la pile.

• le corps d’une fonction/procédure peut modifier les valeurs des registres ``A`` et ``D`` à sa guise. Cela implique que si le programme appelant veut réutiliser la valeur se trouvant dans le registre ``D`` après un appel de fonction/procédure, il devra la sauver sur la pile avant d’exécuter l’instruction ``CALL``.

• toute fonction ou procédure qui ajoute une ou des données sur la pile, doit s’assurer qu’à la fin de son exécution la pile retrouve l’état qu’elle avait avant l’appel à la fonction/procédure.

Nous pouvons facilement écrire le code de la fonction f1 en appliquant ces conventions. Elle prend son argument dans le registre D, l’incrémente et stocke le résultat dans le registre A. Comme elle ne modifie pas les registres B et C, elle ne doit pas les sauver sur la pile.

f1:
        MOV A, D
        INC A
        RET

La fonction f2 fait elle deux appels à la fonction f1. Pour chacun de ces appels, on doit vérifier que l’argument correct est bien placé dans le registre D avant d’exécuter l’instruction CALL. Cela peut se faire en quelques instructions.

f2:        CALL f1
           MOV D, A
           CALL f1
           RET

Nous pouvons maintenant analyser une fonction qui prend deux arguments comme celle qui calcule le minimum entre deux entiers.

Analysons d’abord comment la fonction doit être appelée depuis un programme. Son premier argument doit se trouver dans le registre D et le second doit être sur la pile avant d’exécuter l’instruction CALL min. Le premier argument pourra être calculé ou mis dans le registre D via une instruction MOV. Le second argument est lui placé sur la pile grâce à une instruction PUSH. A ce moment, la fonction min peut être appelée via l’instruction CALL min. Au retour de la fonction min, le registre A contiendra le minimum des deux arguments. Le programme pourra traiter cette valeur minimale comme il le souhaite. Cependant, comme le programme a modifié la pile avant d’appeler la fonction, il ne doit pas oublier de remettre la pile dans son état initial. Cela peut se faire de deux façons:

• en utilisant une instruction POP qui copie la valeur se trouvant au sommet de la pile et incrémente

• en incrémentant simplement le pointeur de sommet de pile (SP) de deux unités

La seconde solution a l’avantage de ne pas modifier de valeur de registre. C’est celle que nous utilisons dans cet exemple. Nous supposons que arg1 et arg2 sont des nombres naturels pour lesquels nous cherchons le minimum.

; appel à la fonction min
MOV D, arg1    ; premier argument
PUSH arg2      ; second argument
CALL min
ADD SP, 2      ; libération de l'argument placé sur la pile

Si nous souhaitons passer comme arguments à la fonction min des valeurs de variables, alors nous devons modifier notre code comme présenté ci-dessous.

; appel à la fonction min
MOV D, [adr1]  ; adresse de la première variable
PUSH [arg2]    ; adresse de la seconde variable
CALL min
ADD SP, 2      ; libération de l'argument placé sur la pile

Nous pouvons maintenant écrire la fonction qui calcule le minimum entre les valeurs de ses deux arguments. Le premier argument se trouve dans le registre D. Il est donc immédiatement disponible. Le second argument lui est sur la pile. Il y a été placé avant l’appel à la fonction via l’instruction CALL min. La figure Fig. 23 présente l’état de la pile à ce moment.

Fig. 23 État de la pile au début de l’exécution de la fonction ``min``

Pour accéder au second argument, il n’est pas intéressant d’utiliser une instruction POP car celle-ci ne permet que d’accéder à l’élément au sommet de la pile, c’est-à-dire l’adresse de retour. Par contre, comme nous savons que l’élément suivant sur la pile se trouve juste au-dessus de cet élément, il nous suffit d’utiliser l’instruction MOV A, [SP+2]. Cette instruction charge dans le registre A la valeur qui se trouve en mémoire à l’adresse correspondant à celle qui est stockée dans le registre SP plus deux unités. Comme un mot de 16 bits en mémoire consomme deux adresses, c’est bien l’adresse de l’élément suivant sur la pile et donc notre second argument. Nous plaçons cet argument dans le registre A car la fonction peut modifier ce registre à sa guise. Ensuite, il suffit de comparer les valeurs se trouvant dans les registres A et D et retourner le minimum dans le registre A. L’instruction RET utilise l’adresse de retour qui se trouve au sommet de la pile.

; calcule le minimum entre les deux valeurs passées en argument


min:
         MOV A,[SP+2] ; second argument copié dans A
         CMP A,D
         JBE finmin
         MOV A,D
finmin:  RET

Dans notre implémentation des fonctions f1 et min, nous avons utilisé la technique du passage par valeur, c’est-à-dire que lorsqu’elle est appelée, une fonction reçoit du programme appelant les valeurs de ses arguments. Ces valeurs sont copiées dans le registre D ou sur la pile par le programme appelant et utilisées par la fonction. Cette technique est utilisée par de nombreux langages de programmation comme python lorsque l’on passe des valeurs d’un type primitif comme des réels ou des entiers à une fonction.

Il existe une seconde technique pour passer les arguments à une fonction. C’est le passage par référence. Dans ce cas, le programme appelant fournit à la fonction qu’il appelle une référence vers son argument. Cette référence est l’adresse en mémoire à laquelle la variable contenant l’argument est stockée. La différence fondamentale entre le passage par référence et le passage par valeur est que comme la fonction connaît l’adresse de la variable contenant son argument, elle peut modifier son contenu alors que c’est impossible avec le passage par valeur. En python, le passage par référence est utilisé lorsque l’argument passé à une fonction est une référence à un objet ou une liste. Il est possible de mixer le passage par référence et le passage par valeur dans une même fonction avec un argument entier passé par valeur et une liste passée par référence.

A titre d’illustration, la fonction inc ci-dessous permet d’incrémenter la variable dont l’adresse est passée par le programme appelant comme argument. Le corps de la fonction inc accède à l’adresse de la variable utilisée par le programme appelant et modifie sa valeur avant de terminer son exécution.

inc:
      MOV A, [D]
      INC A
      MOV [D], A
      RET

En assembleur, on stocke parfois l’information sous la forme d’une séquence de bits. Lorsque les ordinateurs communiquent sur Internet, ils s’échangent les données sous forme de paquets. Chaque paquet est composé d’une entête de quelques dizaines d’octets et suivi des données qui sont échangées. L’entête d’un paquet comprend différents champs dont les valeurs sont fixées par l’émetteur du paquet et qui peuvent être modifiées par les nœuds du réseau (appelés routeurs). A titre d’exemple, la figure ci-dessous présente le format de l’entête d’un paquet IP version 4. Chaque ligne correspond à un mot de 32 bits et l’émetteur d’un tel paquet doit pouvoir spécifier précisément les valeurs de certains bits dans les champs tels que Type of Service ou Flags.

 0                   1                   2                   3
 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
|Version|  IHL  |Type of Service|          Total Length         |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
|         Identification        |Flags|      Fragment Offset    |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
|  Time to Live |    Protocol   |         Header Checksum       |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
|                       Source Address                          |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
|                    Destination Address                        |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
|                    Options                    |    Padding    |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

Notre microprocesseur utilise des mots de 16 bits. Pour traiter une entête de paquet IP, nous devrons donc la découper en blocs de 16 bits qui seront chacun stocké en mémoire ou dans un registre du microprocesseur. Pour faciliter la modification de certains bits en mémoire, nous construisons deux fonctions. Ces fonctions prennent deux arguments :

• la position du bit à modifier (qui est placée dans le registre D suivant notre convention). On supposera que le bit de poids faible est celui qui se trouve en position 0 tandis que le bit de poids fort est en position 15

• le mot de 16 bits à modifier (qui est placé sur la pile suivant notre convention)

Lors de l’exécution de ces fonctions, la pile contient donc l’adresse de retour précédée du mot de 16 bits à modifier comme représenté dans la Fig. 24. Après exécution, nos deux fonctions retournent le mot modifié dans le registre A.

Fig. 24 État de la pile avant l’exécution des fonctions setbit ou resetbit

Notre première fonction est setbit. Elle fixe le nième bit du mot placé sur la pile à la valeur 1. Pour construire cette fonction, il faut se rappeler un peu de logique et utiliser les instructions de décalage. En logique, on se souvient que OR(x,1) vaut toujours 1, quelle que soit la valeur de x. Pour mettre à 1 le bit à l’index 3 d’un mot de seize bits m, il suffit donc de calculer OR(0000000000001000,m). Il nous reste donc à trouver un façon rapide de construire la séquence de bits dont le bit en position n vaut 1 et tous les autres valent 0. Pour cela, il suffit d’utiliser les opérations de décalage. En effet, SHL(0000000000000001,1) donne 0000000000000010. Pour obtenir la séquence 00000000000001000 il suffit d’utiliser l’instruction SHL(0000000000000001,3). En assemblant ces différentes instructions, on obtient le code ci-dessous.

; fonction pour fixer le nième bit d'un mot à 1
; pre: n est dans le registre D et 0<=n<15
; le mot à modifier est sur la pile, retourne le mot
setbit:
   PUSH B ; préservation de la valeur de B
   MOV B, 1
   SHL B, D
   MOV A, [SP+4]
   OR A, B
   POP B  ; récupération de la valeur de B
   RET

De la même façon, on peut aisément construire une fonction pour mettre à zéro le nième bit d’un mot de 16 bits en se rappelant que AND(0,x) vaut toujours 0 et que AND(1,y) vaut y. Pour forcer la valeur du bit en position 4 du mot m, il suffit de calculer AND(111111111101111,m) et 1111111111101111 n’est rien d’autre que NOT(0000000000010000)`. Le code de notre fonction resetbit se déduit facilement.

; fonction pour fixer le nième bit d'un mot à 0
; pre: n est dans le registre D et 0<=n<15
; le mot à modifier est sur la pile, retourne le mot
resetbit:
   PUSH B
   MOV B, 1
   SHL B, D
   NOT B
   MOV A, [SP+4]
   AND A, B
   POP B
   RET

A titre d’exemple, le code ci-dessous teste les fonctions testbit et resetbit.

; exemple d'appel à la fonction set
testset:
   MOV D, 3
   PUSH 2
   CALL setbit
   HLT

; exemple d'appel à la fonction reset
testreset:
   MOV D, 3
   PUSH 14
   CALL resetbit
   HLT

Prenons un autre exemple pour illustrer l’utilisation de la pile et passer plus d’arguments. Construisons la fonction qui calcule l’équivalent de la fonction f qui en python calcule y=a*x+b

def f (x, a, b):
    return a*x+b

En assembleur, nous devons passer les trois arguments à cette fonction en utilisant le registre D pour la valeur de x et la pile pour les valeurs de a et b. Nous devons définir l’ordre dans lequel nous plaçons les arguments sur la pile. Si la valeur de a est passée en premier et celle de b en second, alors lors de l’exécution de notre fonction f, la pile contient les valeurs représentées dans Fig. 25.

Fig. 25 État de la pile durant l’exécution de la fonction f

Nous pouvons ensuite construire notre fonction en utilisant les instructions MOV, MUL et ADD à bon escient.

; calcule y=a*x+b
; x est passé dans le registre D
; a et b sont passés sur la pile
; SP   : adresse de retour
; SP+2 : b
; SP+4 : a
f:
   MOV A, [SP+4] ; récupère x
   MUL D
   ADD A, [SP+2]
   RET

On peut vérifier le bon fonctionnement de cette fonction en exécutant le code ci-dessous:

MOV D, 3
PUSH 4
PUSH 1
CALL f
; A contient 3*4+1
; ne pas oublier de libérer la pile après
ADD SP, 4
HLT

Comme autre exemple d’utilisation de la pile, considérons une fonction qui permet d’ajouter un entier à tous les éléments d’un tableau d’entiers. En python, une telle fonction peut s’écrire comme suit.

def ajouter_entier(entier, tableau):
     for i in range(len(tableau)):
             tableau[i] += entier

Pour traduire cette fonction en assembleur, nous devons déterminer comment passer ses arguments. Nous choisissons de mettre l’entier à ajouter dans le registre D. Pour passer le tableau, nous devons pousser l’adresse du premier élément sur la pile et ensuite la taille du tableau. Au début de l’exécution de la fonction ajouter_entier, la pile contient donc les informations reprises en Fig. 26.

Fig. 26 État de la pile au début de l’exécution de la fonction ajouter_entier

Notre fonction va utiliser les registres B et C. Nous devons donc d’abord les sauvegarder sur la pile. Durant l’exécution de la fonction ajouter_entier, la pile contiendra donc les informations reprises en Fig. 27.

Fig. 27 État de la pile pendant l’exécution de la fonction ajouter_entier

La fonction peut ensuite aisément se traduire en assembleur comme une boucle qui itère sur tous les éléments du tableau. Il faut cependant être attentif à correctement charger l’adresse du tableau et sa taille depuis la pile. Comme nos entiers sont stockés sur 16 bits, nous devons aussi incrémenter l’adresse du prochain élément de deux unités à chaque passage dans la boucle.

; ajoute son premier argument à tous les éléments du tableau
; registre D: x, valeur à ajouter
; SP+4 : adresse du premier élément du tableau
; SP+2 : nombre d'éléments
ajouter_entier:
   PUSH B ; préservation du contenu de B
   PUSH C ; préservation du contenu de C
   MOV B, [SP+8] ; adresse du tableau
   MOV C, [SP+6] ; nombre d'éléments
loop:
   MOV A, D
   ADD A, [B] ; calcule de tableau[i]+entier
   MOV [B], A ; sauvegarde du résultat en mémoire
   ADD B, 2 ; adresse suivante
   DEC C
   CMP C, 0
   JNE loop
   POP B ; récupération du contenu de B
   POP C ; récupération du contenu de C
   RET

Cette fonction peut être testée en créant un tableau contenant quelques entiers et en appelant la fonction comme dans l’exemple ci-dessous.

; création d'un tableau de 5 entiers
t: DB 1
   DB 2
   DB 3
   DB 4
   DB 5
   MOV D, 3 ; valeur à ajouter
   PUSH t   ; adresse du premier élément du tableau
   PUSH 5   ; nombre d'éléments
   CALL ajouter_entier

Nous devons maintenant trouver une réponse à la troisième question. Lors de son exécution, une fonction doit souvent utiliser de la mémoire, pour stocker des résultats intermédiaires de calculs ou des variables locales. C’est le cas de la fonction fct dans l’exemple en python ci-dessous. Celle-ci a besoin de mémoire pour réaliser les calculs qui se trouvent dans son corps. Il en va de même par exemple pour une fonction qui contiendrait une simple boucle.

# retourne x+2*y si x<y et y-5*x sinon
def fct(x,y):
    if (x<y):
        r=x+2*y
    else:
        r=y-5*x
    return(r)

Chacune des variables locales d’une fonction doit être stockée à une adresse mémoire. Une première approche naïve pour résoudre ce problème serait de réserver une zone de mémoire fixe pour les variables locales utilisées par chaque fonction. Dans une implémentation en assembleur de l’exemple ci-dessus, on pourrait réserver une adresse en mémoire RAM pour la variable r de la fonction fct. Malheureusement, cette approche a deux inconvénients. Premièrement, toute la mémoire qu’une fonction peut utiliser durant son exécution doit être réservée en RAM avant de pouvoir exécuter cette fonction. Si une fonction doit utiliser un grand tableau lorsqu’elle est appelée avec une valeur spécifique d’un argument, alors la zone nécessaire pour ce tableau doit toujours être réservée, même si la fonction n’est jamais exécutée par le programme. Le deuxième inconvénient est qu’il est impossible avec cette approche de supporter une fonction f qui appelle une fonction g qui elle-même appelle une fonction f car le premier appel à la fonction f aura initialisé les « variables locales de la fonction f » puis fera appel à la fonction g. Lorsque g fait appel de son côté à la fonction f, cette seconde invocation de la fonction f va modifier les données stockées aux adresses en mémoire qui correspondent à ses variables locales et donc modifier les variables utilisées par la première invocation de la fonction f. Si ce second inconvénient peut paraître un peu théorique et hypothétique à ce stade, il est malheureusement bien réel en pratique.

On peut éviter ces deux inconvénients en utilisant la pile comme mémoire pour stocker les variables locales d’une fonction. La pile n’utilise la RAM que durant l’exécution de la fonction, il n’y a donc pas de gaspillage de mémoire comme avec la solution précédente. Dans le cas où une invocation de la fonction f appelle la fonction g qui appelle elle-même la fonction f, le bas de la pile contiendra les arguments, adresse de retour et variables de la première invocation de la fonction f. Au-dessus de ces informations, on trouvera les arguments, adresses de retour et variables locales de la fonction g. Enfin, les arguments, adresse de retour et variables locales de la seconde invocation de la fonction f sont au sommet de la pile. A la fin de son exécution, cette invocation de la fonction f libère la mémoire qu’elle utilise sur la pile.

La meilleure illustration de l’utilisation de la pile par les fonctions en assembleur est le support des fonctions récursives. En informatique, on parle de récursion lorsqu’une fonction s’appelle elle-même. C’est le cas par exemple de la fonction sumn qui permet de calculer la somme des n premiers naturels.

# Somme des n premiers naturels
def sumn(n):
    if(n==0):
        return(0)
    return(n+sumn(n-1))

print(sumn(1)) # affiche 1
print(sumn(3)) # affiche 6

En assembleur, cette fonction peut s’appeler en plaçant simplement la valeur de la variable n dans le registre D en utilisant le code ci-dessous.

MOV D, [n]
CALL sumn
; résultat dans le registre A

Le code de la fonction sumn en assembleur comprend deux parties principales : le cas de base (n==1) et le cas récursif. Pour la partie récursive, nous devons calculer n+sum(n-1). Pour cela, il est nécessaire de placer la valeur de n-1 dans le registre D pour appeler la fonction sumn tout en gardant la valeur de n pour pouvoir calculer la somme n+sum(n-1). Cela nécessite d’utiliser le registre B à l’intérieur de notre fonction. C’est pour cette raison que nous sauvegardons ce registre via l’instruction PUSH B au début du code de la fonction. Nous plaçons également une instruction POP B pour récupérer la valeur placée sur la pile juste avant d’exécuter l’instruction RET.

sumn:
        PUSH B   ; sauvegarde
        CMP D,1
        JNE recursif
        MOV A, D ; n==1, return(n)
        POP B    ; récupération
        RET
recursif:
        MOV B, D ; on aura besoin de n après
        DEC D
        CALL sumn ; appel récursif
rec2:
        ADD A, B  ; résultat dans A
        POP B
        RET

Pour bien comprendre le fonctionnement d’un tel programme récursif et son utilisation de la pile, il est intéressant d’observer son exécution pas à pas en parallèle avec l’évolution de la pile. Cette fonction est appelée par le code suivant:

    MOV B, 17
    MOV D, 3
    CALL sumn
RETOUR:

La Fig. 28 présente l’état de la pile lors de l’appel à la fonction sumn avec 3 comme argument. Par convention, le sommet de la pile se trouve en bas de la figure et utilise une police de caractères grasse.

Fig. 28 Contenu de la pile lors de l’appel à la fonction sumn(3)

Durant son exécution, cette fonction sauvegarde d’abord le registre B puis fait appel à sumn(2). La Fig. 29 présente l’état de l’appel au moment de cet appel.

Fig. 29 Contenu de la pile lors de l’appel à sumn(2)

Lors de son exécution, l’invocation de la fonction sumn avec 2 comme argument va d’abord faire appel à sumn(1). La Fig. 30 présente l’état de la pile au moment de cet appel.

Fig. 30 Contenu de la pile lors de l’appel à sumn(1)

Lors de son exécution, l’invocation de la fonction sumn avec 1 comme argument va d’abord sauvegarder le registre B sur la pile. La Fig. 31 présente l’état de la pile au moment de cet appel.

Fig. 31 Contenu de la pile durant l’exécution de sumn(1)

Nous sommes maintenant dans l’exécution de la fonction sumn(1). Celle-ci retourne la valeur 1 dans le registre A et retire le mot se trouvant au sommet de la pile. Elle retourne à l’adresse RETSUMN avec la pile dans l’état représenté à la Fig. 30. Grâce à cette pile, la fonction sumn récupère son argument (1) et retourne la valeur 1 qui est la somme entre la valeur du registre B et son argument. A la fin de son exécution, cette invocation de la fonction sumn retire les deux mots qui se trouvaient au sommet de la pile.

L’état de la pile est maintenant celui de la Fig. 29 et le registre A contient la valeur 1. Nous sommes dans la dernière partie de l’invocation de la fonction sumn(2). Celle-ci calcule son résultat (3) et retire les deux mots se trouvant au sommet de la pile avant de faire un saut à l’adresse RETSUMN.

Nous sommes maintenant dans l’invocation de la fonction sumn(3). L’état de la pile est celui de la Fig. 28. La fonction récupère l’argument (3) et l’ajoute au résultat de la fonction appelée qu’elle a reçu dans le registre A (3). Le registre D contient maintenant le résultat final (6) de l’appel sumn(3). Il ne reste plus qu’à retirer les deux mots se trouvant au sommet de la pile et retourner à l’adresse RETOUR dans le programme appelant.

En utilisant la même approche, on peut construire une implémentation en assembleur de la fonction qui permet de calculer la factorielle d’un naturel.

; Calcul de la factorielle d'un naturel, argument dans D, résultat dans A

fact:
      PUSH B
      CMP D,1
      JNE suite
      MOV A, D
      POP B
      RET
suite:
  MOV B, D
  DEC D
      CALL fact
      MUL B
      POP B
      RET