Langage d’assemblage

Avec la mémoire et l’ALU nous avons les briques de base qui vont nous permettre de construire un micro-processeur qui sera capable d’exécuter de petits programmes. Ce micro-processeur répond à ce que l’on appelle l”architecture de Von Neumann.

Cette architecture est composée d’un processeur (CPU en anglais) ou unité de calcul et d’une mémoire. Le processeur est un circuit électronique qui est capable d’effectuer de nombreuses tâches :

  • lire de l’information en mémoire

  • écrire de l’information en mémoire

  • réaliser des calculs

L’architecture des ordinateurs est basée sur l’architecture dite de Von Neumann. Suivant cette architecture, un ordinateur est composé d’un processeur qui exécute un programme se trouvant en mémoire. Ce programme manipule des données qui sont aussi stockées en mémoire.

Dans notre minuscule ordinateur, toutes les informations sont stockées sous la forme de nombres binaires. Le livre a fait le choix d’utiliser des mots de 16 bits comme unité de base pour les calculs et la mémoire. On pourrait dire que notre minuscule ordinateur est un ordinateur « 16 bits ». Ce choix a plusieurs conséquences sur les données qui sont traitées par ce minuscule processeur:

  • les entiers sont représentés en utilisant la notation binaire en complément à deux sur 16 bits

  • chaque caractère ASCII est également stocké sous la forme d’un nombre sur 16 bits

Notre minuscule processeur ne supporte pas les nombres réels. L’utilisation de 16 bits pour représenter chaque caractère constitue un gaspillage de la mémoire puisqu’il suffit d’utiliser 8 bits pour représenter les caractères ASCII. Cependant, ce gaspillage de mémoire permet de simplifier fortement l’implémentation de notre minuscule processeur comme vous le verrez dans le prochain projet. On ne peut pas gagner de tous les points de vue.

Les ordinateurs actuels sont basés sur d’autres choix. Les entiers sont encodés sur 32 ou 64 bits tandis que les caractères sont soit encodés sur 8 bits lorsque l’on utilise la représentation ASCII historique soit sur 16 bits pour la représentation Unicode.

Le minuscule ordinateur construit dans le livre de référence a d’autres caractéristiques particulières qui simplifient sa réalisation mais ne correspondent pas nécessairement aux ordinateurs actuels. Ce minuscule ordinateur utilise deux mémoires séparées :

  • une mémoire dite mémoire d’instructions contenant le code des programmes à exécuter

  • une mémoire dite mémoire de données contenant les données à traiter

Ces deux mémoires ont chacune une capacité de 16384 mots de 16 bits. La plupart des ordinateurs actuels utilisent une mémoire qui contient indifféremment les données et le code machine des programmes. La mémoire d’instructions de notre minuscule ordinateur est une mémoire de type ROM. Elle est initialisée au lancement de l’ordinateur avec le programme à exécuter mais ne peut pas être modifiée par un programme. La mémoire de données elle est une mémoire de type RAM dans laquelle les programmes peuvent lire et écrire des données.

Une autre différence entre le minuscule ordinateur et un ordinateur actuel est la façon dont on accède aux données en mémoire. Le minuscule ordinateur peut uniquement lire ou écrire un mot de 16 bits à la fois à une adresse donnée en mémoire de données. Un ordinateur actuel peut lire et écrire un octet en mémoire, un mot de 16, 32 ou 64 bits voire beaucoup plus dans certains cas.

Outre ces deux mémoires, notre minuscule processeur dispose de deux registres :

  • le premier, baptisé D est utilisé pour stocker un mot de 16 bits qui est lu depuis la mémoire ou résulte d’un calcul réalisé par l’ALU. Son nom reflète le fait qu’il stocke des données (Data en anglais)

  • le second, baptisé A. Il a un double rôle. Tout d’abord, va il servir à stocker une donnée sur 16 bits comme le registre D. Son deuxième rôle est de contenir une adresse dans la mémoire de données pour permettre le chargement d’une donnée depuis cette mémoire. C’est pour cette raison qu’il est appelé le registre A (comme adresse).

Ces deux registres A et D sont schématiquement connectés à l’ALU qui est le coeur de notre minuscule processeur. Cela permet d’utiliser l’ALU pour réaliser différents calculs sur ces deux registres (Fig. 109).

[ reg/.style={rectangle, draw, minimum width=2.7 cm} ] \node[reg] (output) at (2,0) {\small sortie [16 bits]}; \node[reg] (D) at (-3,0.5) {\small D [16 bits]}; \node[reg] (A) at (-3,-0.5) {M/A [\small 16 bits]}; \draw (-0.75,-1) -- (-0.75, 1) -- (0,0.35) -- (0,-0.35) -- cycle; \draw[->] (A.east) -- (-0.5,-0.5); \draw[->] (D.east) -- (-0.5,0.5); \draw[->] (0,0) -- (output.west);

Fig. 109 Les registres A, D et l’ALU

A côté de ces deux registres qui sont associés aux données, notre minuscule processeur contient également un registre baptisé PC (pour Program Counter ou compteur de programmes). Ce registre contient l’adresse de l’instruction qui est exécutée par le minuscule processeur. Nous verrons plus tard comment celui-ci est utilisé.

Les instructions du minuscule processeur

Avant de construire le minuscule processeur dans le projet suivant, nous devons d’abord comprendre quelles sont les instructions que celui-ci peut exécuter. Il supporte deux types d’instructions qui sont toutes les deux encodées sous la forme d’un mot de 16 bits.

L’instruction de type A

L’instruction la plus simple du minuscule microprocesseur est l’instruction de type A (où A est l’abréviation de adresse). Cette instruction permet simplement de charger un nombre binaire sur 15 bits dans le registre A. Dans les logiciels fournis avec le livre de référence, cette instruction s’écrit @ suivi de la valeur à placer dans le registre A. La valeur passée comme argument de cette instruction de type A est obligatoirement un entier positif. Nous verrons plus tard comment indiquer une constante négative.

@1           // charge la valeur 1 dans A
@123         // charge la valeur 123, i.e. 1111011 en binaire dans A

Vous pouvez télécharger cet exemple depuis asm/ex0.asm.

Cette instruction a trois utilisations en pratique. Tout d’abord, elle permet de charger une valeur constante dans le registre A. Mais surtout elle est utilisée avec les instructions de type C pour soit indiquer une adresse mémoire à laquelle une donnée doit être chargée soit une adresse mémoire où un saut doit être réalisé si une condition est vérifiée. Nous y reviendrons.

Comme toutes les instructions, l’instruction de type A est encodée sous la forme d’un mot de 16 bits. L’encodage est extrêmement simple :

  • le bit de poids fort est mis à 0

  • les quinze bits de poids faible sont la valeur de l’argument de l’instruction en binaire

C’est à cause de l’encodage de l’instruction dans un mot de 16 bits que la constante qui est passée en argument doit être encodée sur 15 bits.

L’instruction de type C

Cette instruction est l’instruction « à tout faire » du minuscule processeur. Son nom vient de l’initiale de Compute (calculer). C’est elle qui permet d’utiliser toutes les fonctionnalités de l’ALU mais aussi d’implémenter des instructions conditionnelles et des boucles comme nous le verrons par après.

Plutôt que de présenter directement toutes les possibilités de cette instruction, nous allons la construire petit à petit sur base d’exemples illustratifs. Une première utilisation de l’instruction de type C est de charger des données depuis la mémoire vers un registre ou d’un registre vers la mémoire. Cette variante de l’instruction C s’écrit généralement sous la forme \(dest = calcul\). Nous verrons plus tard comment réaliser un calcul en utilisant l’ALU. Commençons par observer le fonctionnement de cette instruction. La partie gauche de l’instruction de type C indique l’endroit où le résultat de notre calcul doit être stocké. La première destination possible est le registre D. Une deuxième destination possible est le registre A. Enfin, la troisième destination possible pour le résultat d’un calcul de l’ALU est la mémoire. Dans le minuscule assembleur, ceci est représenté en utilisant le symbole M. Ce symbole est un raccourci pour représenter le mot de 16 bits en mémoire se trouvant à l’adresse contenue dans le registre A. Ces trois destinations peuvent être combinées entre elles. La partie gauche de l’instruction de type C peut contenir les symboles suivants :

  • D le résultat du calcul doit être stocké dans le registre D

  • A le résultat du calcul doit être stocké dans le registre A

  • M le résultat du calcul doit être stocké dans la mémoire à l’adresse qui se trouve actuellement dans le registre A

  • MD le résultat du calcul doit être stocké dans le registre D et dans la mémoire à l’adresse qui se trouve actuellement dans le registre A

  • AM le résultat du calcul doit être stocké dans le registre A et dans la mémoire à l’adresse qui se trouve actuellement dans le registre A

  • AD le résultat du calcul doit être stocké dans le registre A et dans le registre D

  • AMD le résultat du calcul doit être stocké dans le registre A, le registre D et dans la mémoire à l’adresse qui se trouve actuellement dans le registre A

Il est aussi possible d’avoir une instruction de type C qui ne modifie ni les registres A/D ni la mémoire. Nous en parlerons plus tard.

La partie droite de l’instruction de type C permet de spécifier le calcul à réaliser. Une première possibilité est de prendre la valeur d’un registre ou d’une zone mémoire sans demander à l’ALU de réaliser un calcul particulier. Les trois calculs les plus simples à réaliser correspondent aux symboles A, D et M :

  • D le résultat du calcul est la valeur stockée dans le registre D

  • A le résultat du calcul est la valeur stockée dans le registre A

  • M le résultat du calcul est la donnée qui se trouve en mémoire à l’adresse qui se trouve actuellement dans le registre A

Nous pouvons maintenant explorer ces différentes instructions. Supposons que la mémoire contient les valeurs reprises dans Tableau 11.

Tableau 11 Contenu de la mémoire

adresse

valeur

0

9

1

2

2

4

3

1

Commençons par le code qui permet de charger une donnée en mémoire.

@1     // place l'adresse 1 dans le registre A
D=M    // lit la donnée à l'adresse 1 en mémoire et la place dans D

Après exécution de ces deux instructions, le registre D contient la valeur qui se trouvait en mémoire à l’adresse 1, c’est-à-dire 2.

Vous pouvez télécharger cet exemple depuis asm/ex1.asm.

Notre deuxième exemple montre qu’il est aussi possible de charger le registre A avec une valeur stockée en mémoire.

@1     // place l'adresse 1 dans le registre A
A=M    // lit la donnée à l'adresse 1 en mémoire et place donc (2) dans A
D=M    // lit la donnée à l'adresse 2 en mémoire (4) et la place dans D

Vous pouvez télécharger cet exemple depuis asm/ex2.asm.

Notre troisième exemple montre comment déplacer une information en mémoire.

@3     // place l'adresse 3 dans le registre A
AD=M   // lit la donnée à l'adresse 3 en mémoire (1) et la place dans A et D
@0     // place l'adresse 0 dans le registre A
M=D    // sauve la donnée se trouvant dans D en mémoire à l'adresse se trouvant dans A (0)

Vous pouvez télécharger cet exemple depuis asm/ex3.asm.

Nous pouvons maintenant utiliser ces instructions pour réaliser des initialisations de variables comme dans un langage de haut niveau comme python. En python cette initialisation s’écrit comme en Code source 4

Code source 4 Initialisation de variables en python
a=1
b=42

Avant de pouvoir initialiser des variables en assembleur, nous devons d’abord définir l’adresse en mémoire à laquelle chaque variable est stockée. Par convention, le minuscule processeur réserve les adresses de 0 à 15 en mémoire de données pour certaines utilisations particulières. Nous pouvons donc stocker nos variables à partir de l’adresse 16. Nous pouvons par exemple placer la variable a à l’adresse 16 et la variable b à l’adresse 17. Dans un programme en assembleur, on définit généralement une table des symboles qui associent une adresse à chaque variable du programme. Dans notre exemple, cette table des symboles pourrait être celle du Tableau 12.

Tableau 12 Table des symboles

adresse

variable

16

a

17

b

18

…

Pour initialiser ces variables, la séquence d’instruction à utiliser est la suivante. Premièrement, il faut charger la valeur 1 dans le registre D. Ensuite il faut charger dans le registre A l’adresse de la variable a (16 dans notre exemple) pour pouvoir sauver le contenu du registre D à cette adresse en mémoire. On fait de même pour l’initialisation de la variable b.

Code source 5 Initialisation de variables en assembleur
@1    // valeur 1 pour l'initialisation
D=A
@16   // adresse de la variable a
M=D
@42   // valeur 42 pour l'initialisation
D=A
@17   // adresse de la variable b
M=D

Vous pouvez télécharger cet exemple depuis asm/ex4.asm.

Dans un programme python, il est parfois nécessaire d’échanger le contenu de la variable a avec celui de la variable b. En python, cela peut se faire de deux façons. La première solution est d’utiliser une variable intermédiaire (Code source 6)

Code source 6 Echange de contenu de variables en python
x=a
a=b
b=x

Pour simplifier la vie du programmeur, python permet de cacher la création d’une variable temporaire et supporte la forme compacte reprise en Code source 7.

Code source 7 Echange de contenu de variables en python (forme compacte)
a,b = b, a

Pour faire la même opération en langage assembleur, nous devons aussi passer par une zone mémoire intermédiaire. Dans notre exemple, l’adresse 18 est inutilisée. Nous pouvons donc y placer le contenu de la variable b avant d’y copier le contenu de la variable a comme dans le programme en python. La code assembleur est présenté en Code source 8.

Code source 8 Echange du contenu de variables en assembleur
@17   // variable b
D=M
@18   // variable x
M=D
@16   // variable a
D=M
@17   // variable b
M=D
@18   // variable x
D=M
@16   // variable b
M=D

Vous pouvez télécharger cet exemple depuis asm/ex5.asm.

Continuons notre exploration des instructions de type C. L’ALU de notre minuscule processeur est aussi capable de produire les constantes suivantes :

  • 0

  • 1

  • -1

Ces constantes peuvent apparaître dans la partie de droite d’une instruction de type C. A titre d’exemple le Code source 9 initialise le contenu de la variable x à la valeur 1 et celui de la variable y à -1.

Code source 9 Initialisation de variables
@20   // variable x
M=1
@21   // variable y
M=-1

Vous pouvez télécharger cet exemple depuis asm/ex6.asm.

Notre minuscule ALU peut aussi réaliser des calculs sur un registre ou une valeur lue en mémoire. La partie de droite d’une instruction de type C peut en effet contenir les symboles suivants:

  • !D : le résultat de l’ALU sera le résultat de l’application de l’opération NOT à tous les bits du contenu du registre D

  • !A : le résultat de l’ALU sera le résultat de l’application de l’opération NOT à tous les bits du contenu du registre A

  • !M : le résultat de l’ALU sera le résultat de l’application de l’opération NOT à tous les bits du mot lu en mémoire à l’adresse contenue dans le registre A

  • -D : le résultat de l’ALU sera l’opposé du contenu du registre D

  • -A : le résultat de l’ALU sera l’opposé du contenu du registre A

  • -M : le résultat de l’ALU sera l’opposé du mot lu en mémoire à l’adresse contenue dans le registre A

  • D+1 : le résultat de l’ALU sera le contenu du registre D incrémenté de 1

  • A+1 : le résultat de l’ALU sera le contenu du registre A incrémenté de 1

  • M+1 : le résultat de l’ALU sera le mot lu en mémoire à l’adresse contenue dans le registre A incrémenté de 1

  • D-1 : le résultat de l’ALU sera le contenu du registre D décrémenté de 1

  • A-1 : le résultat de l’ALU sera le contenu du registre A décrémenté de 1

  • M-1 : le résultat de l’ALU sera le mot lu en mémoire à l’adresse contenue dans le registre A décrémenté de 1

Enfin, il est possible d’utiliser l’ALU pour effectuer des opérations arithmétiques (addition et soustraction) et logiques (AND et OR) avec les registres A et D ainsi que le mot lu en mémoire à l’adresse se trouvant dans le registre A. Le minuscule processeur supporte six opérations arithmétiques.

  • A+D : le résultat de l’ALU sera le résultat de l’addition du contenu du registre D et du contenu du registre A

  • D+M : le résultat de l’ALU sera le résultat de l’addition du contenu du registre D et du mot lu en mémoire à l’adresse contenue dans le registre A

  • A-D : le résultat de l’ALU sera le résultat de la soustraction du contenu du registre A moins le contenu du registre D

  • D-A : le résultat de l’ALU sera le résultat de la soustraction du contenu du registre D moins le contenu du registre A

  • D-M : le résultat de l’ALU sera le résultat de la soustraction du contenu du registre D moins le mot lu en mémoire à l’adresse contenue dans le registre A

  • M-D : le résultat de l’ALU sera le résultat de la soustraction du mot lu en mémoire à l’adresse contenue dans le registre A moins le contenu du registre D

Les dernières opérations supportées par l’ALU sont les opération logiques.

  • D&A : le résultat de l’ALU sera le résultat de l’opération logique AND appliquée au contenu du registre D et au contenu du registre A

  • D|A : le résultat de l’ALU sera le résultat de l’opération logique OR appliquée au contenu du registre D et au contenu du registre A

  • D&M : le résultat de l’ALU sera le résultat de l’opération logique AND appliquée au contenu du registre D et au mot lu en mémoire à l’adresse contenue dans le registre A

  • D|M : le résultat de l’ALU sera le résultat de l’opération logique OR appliquée au contenu du registre D et au mot lu en mémoire à l’adresse contenue dans le registre A

Avec ces 28 opérations, nous pouvons maintenant réaliser de très nombreuses opérations arithmétiques et logiques. Dans un programme informatique, il est très courant de devoir incrémenter ou décrémenter une variable. Dans notre minuscule langage d’assemblage, cette opération peut se réaliser de différentes façons. Une première solution pour incrémenter une variable est d’y ajouter la constante 1. Supposons que notre variable soit stockée à l’adresse 20.

Code source 10 Incrémentation de la valeur d’une variable en assembleur
@20   // adresse de la variable
D=M   // chargement de la valeur de la variable
@1    // constante 1
D=D+A // addition
@20   // adresse de la variable
M=D   // sauvegarde du résultat en mémoire

Vous pouvez télécharger cet exemple depuis asm/ex7.asm.

Il existe une solution nettement plus compacte et plus efficace (Code source 11).

Code source 11 Incrémentation de la valeur d’une variable en assembleur
@20   // adresse de la variable
M=M+1

Vous pouvez télécharger cet exemple depuis asm/ex7b.asm.

Il en va de même pour décrémenter la valeur d’une variable (Code source 12).

Code source 12 Décrémentation d’une variable en assembleur
@20   // adresse de la variable
M=M-1

Vous pouvez télécharger cet exemple depuis asm/ex7c.asm.

Le minuscule langage d’assemblage permet de réaliser des opérations mathématiques plus complexes. il est en effet possible de combiner des additions et des soustractions. Supposons que A, B et C sont des variables entières et qu’il faut calculer \(A+B-C\) et stocker le résultat dans la variable :math`X`. Pour cela, il faut d’abord fixer les adresses mémoires dans lesquelles ces variables sont stockées (Tableau 13).

Tableau 13 Table des symboles

adresse

variable

21

A

22

B

23

C

25

X
Code source 13 X=A+B-C en assembleur minuscule
@21   // adresse de la variable A
D=M   // chargement de la valeur de la variable
@22   // adresse de la variable B
D=D+M // addition, D contient A+B
@23   // adresse de la variable C
D=D-M // soustraction, D contient A+B-C
@25   // adresse de la variable X
M=D   // sauvegarde du résultat en mémoire

Vous pouvez télécharger cet exemple depuis asm/ex8.asm.

On peut également utiliser les instructions de notre langage d’assemblage pour calculer l’opposé d’un nombre. Si la variable est stockée à l’adresse 20 et que son opposé doit être stocké à l’adresse 24, une première solution est de procéder comme dans le Code source 14.

Code source 14 Calcul de l’opposé
@20   // adresse de la variable
D=-M  // calcul de l'opposé
@24   // adresse de la variable B
M=D   // sauvegarde du résultat en mémoire

Vous pouvez télécharger cet exemple depuis asm/ex9.asm.

Exercices

  1. Proposez deux façons pour initialiser la variable X qui est stockée à l’adresse 23 à la valeur 17.

  2. Avec le minuscule langage d’assemblage, comment faire pour initialiser une variable à la valeur -2 ?

  3. Que font les instructions en assembleur minuscule ci-dessous ?

    @20
D=!M
D=D+1
@25
M=D

  1. Avec le minuscule assembleur, l’initialisation d’une variable se fait normalement avec une instruction de type A :

@1234   // valeur
D=A
@16     // adresse variable
M=D

Cependant, comme l’instruction de type A est encodée sur 16 bits, il n’y a que 15 bits de disponibles pour encoder cette valeur. Comment feriez-vous pour traduire l’assignation x=50000 en minuscule assembleur ?

  1. Le minuscule assembleur supporte les opérations logiques AND et OR de l’ALU. Certains langages de programmation supportent également l’opération XOR. Comment feriez-vous pour implémenter l’opération XOR en minuscule assembleur ?

Toutes les instructions de type C sont encodées sous la forme d’un mot de 16 bits qui a la structure suivante :

\(1 1 1 a c_1 c_2 c_3 c_4 c_5 c_6 d_1 d_2 d_3 j_1 j_2 j_3\)

Dans cette structure, le bit de poids fort mis à 1 permet au minuscule processeur de distinguer une instructions de type A (dont le bit de poids fort est mis à 0) d’une instruction de type C. Les deux bits suivants ne sont pas utilisés par le minuscule processeur. Ensuite, les bits a et \(c_i\) servent à spécifier les différentes instructions que nous avons présenté ci-dessus. Le livre de référence contient la spécification complète de ces instructions. En voici quelques unes à titre d’exemples. Pour les instructions arithmétiques et logiques, les bits de poids faible (\(j_1 j_2 j_3\) sont mis à 0).

  • l’instruction M=D+1 a comme encodage 1 1 1 0 0 1 1 1 1 1 0 0 1 0 0 0. Dans cet encodage, 0 0 1 1 1 1 1 représente le membre de droite (D+1) et 0 0 1 le membre de gauche de l’instruction

  • l’instruction D=D+1 a comme encodage 1 1 1 0 0 1 1 1 1 1 0 1 0 0 0 0. Dans cet encodage, 0 0 1 1 1 1 1 représente le membre de droite (D+1) et 0 1 0 le membre de gauche de l’instruction

  • l’instruction AMD=A-D a comme encodage 1 1 1 0 0 0 0 1 1 1 1 1 1 0 0 0. Dans cet encodage, 0 0 0 0 1 1 1 représente le membre de droite (A-D) et 1 1 1 le membre de gauche de l’instruction

Le rôle des autres bits qui composent cette instruction sera détaillé plus tard.

Les instructions de saut

Pour exécuter un programme, notre minuscule processeur doit charger une nouvelle instruction à chaque cycle d’horloge. Il le fait en utilisant le registre PC. Celui-ci est initialisé à la valeur 0 lorsque le minuscule processeur démarre. A chaque cycle d’horloge, le minuscule processeur réalise les opérations suivantes :

  • lecture de l’instruction se trouvant à l’adresse qui est stockée dans le registre PC

  • décodage de l’instruction lue en mémoire

  • exécution de l’instruction lue en mémoire

  • mise à jour du registre PC

L’exécution de toutes les instructions que nous avons vues jusque maintenant se termine par l’incrémentation du contenu du registre PC. Cela permettra à notre minuscule processeur de charger automatiquement l’instruction suivante lors du prochain cycle d’horloge.

L’encodage de l’instruction de type C implique que les trois bits de poids faible (\(j_1 j_2 j_3\)) restent disponibles. Ceux-ci vont nous permettre de supporter les instructions conditionnelles (if ... else) et les boucles. Pour comprendre comment ces instructions sont supportées en langage d’assemblage, nous devons d’abord comprendre comment fonctionne le compteur de programme (ou Program Counter - PC en anglais). Ce compteur de programme est un registre qui fait partie de notre minuscule processeur et qui contient à tout instant l’adresse de l’instruction que le minuscule processeur exécute. Reprenons le code du calcul de l’opposé (Code source 14). Ce code contient quatre instructions. Il est stocké dans la mémoire d’instructions (Tableau 14).

Tableau 14 Instructions du calcul de l’opposé en mémoire d’instructions

adresse

instruction

51

@20

52

D=-M

53

@24

54

M=D

Pour exécuter ces instructions en mémoire d’instructions, le PC prend d’abord la valeur 51. Le minuscule processeur exécute à ce moment l’instruction @20. A la fin de l’exécution de cette instruction, le PC est incrémenté d’une unité et passe à 52. Il exécute ensuite l’instruction D=-M. A la fin de l’exécution de cette instruction, le PC passe à la valeur 53 et ainsi de suite.

Les trois bits de poids faible de l’instruction de type C permettent d’influencer la façon dont le contenu du PC est modifié à la fin de l’exécution de l’instruction en cours. Lorsque ces trois bits valent 0 0 0, le PC est incrémenté d’une unité. Si par contre ces trois bits valent 1 1 1, le PC prend la valeur qui se trouve dans le registre A pour réaliser un saut (jump en anglais). Pour comprendre l’utilisation de ces sauts, revenons aux instructions qui nous permettent d’incrémenter une variable en mémoire (Code source 11). Supposons que notre variable est stockée à l’adresse 22 en mémoire de données et que notre séquence d’instructions commence à l’adresse 71 en mémoire d’instructions.

Tableau 15 Un programme qui ne s’arrête jamais

adresse

instruction

71

@22

72

M=M+1

73

@71

74

0;JMP

Vous pouvez télécharger cet exemple depuis asm/ex10.asm.

Exécutons le programme représenté en Tableau 15 instruction par instruction en supposant que la mémoire de données contient initialement la valeur 0 à l’adresse 22. Les instructions suivantes sont exécutées :

  • exécution de l’instruction à l’adresse 71, chargement de la valeur 22 dans le registre A, PC passe à 72

  • exécution de l’instruction à l’adresse 72, incrémentation de la valeur stockée en mémoire à l’adresse se trouvant dans le registre A. L’adresse 22 en mémoire de données contient maintenant 1. PC passe à 73

  • exécution de l’instruction à l’adresse 73, chargement de la valeur 71 dans le registre A, PC passe à 74

  • exécution de l’instruction à l’adresse 74, le PC prend la valeur stockée dans le registre A (71)

  • exécution de l’instruction à l’adresse 71, chargement de la valeur 22 dans le registre A (1), PC passe à 72

  • exécution de l’instruction à l’adresse 72, incrémentation de la valeur stockée en mémoire à l’adresse se trouvant dans le registre A. L’adresse 22 en mémoire de données contient maintenant 2. PC passe à 73

  • exécution de l’instruction à l’adresse 73, chargement de la valeur 71 dans le registre A, PC passe à 74

  • exécution de l’instruction à l’adresse 74, le PC prend la valeur stockée dans le registre A (71)

  • …

Ce programme ne s’arrêtera jamais. Il est équivalent au code python suivant.

while True:
  x=x+1

Les instructions de saut conditionnel

L’instruction de saut (0;JMP) est très fréquente en assembleur. Elle permet d’effectuer un saut qui est dit non-conditionnel car la valeur du PC est toujours modifiée. A côté de cette instruction, notre minuscule langage d’assemblage supporte plusieurs instructions de saut conditionnel. Ces instructions modifient la valeur du PC uniquement si une condition particulière est vérifiée. Le langage d’assemblage du minuscule processeur supporte six instructions de saut conditionnel :

  • JEQ (Jump if EQual to 0). Avec cette instruction, le saut est réalisé uniquement si le résultat du calcul fait par l’ALU est nul.

  • JNE (Jump if Not Equal to 0). Avec cette instruction, le saut est réalisé uniquement si le résultat du calcul fait par l’ALU est différent de zéro.

  • JGT (Jump if Greater Than 0). Avec cette instruction, le saut est réalisé uniquement si le résultat du calcul fait par l’ALU est strictement positif.

  • JLT (Jump if Lower Than 0). Avec cette instruction, le saut est réalisé uniquement si le résultat du calcul fait par l’ALU est strictement inférieur à 0.

  • JGE (Jump if Greater than or Equal to 0). Avec cette instruction, le saut est réalisé uniquement si le résultat du calcul fait par l’ALU est supérieur ou égal à 0.

  • JLE (Jump if Lower than or Equal to 0). Avec cette instruction, le saut est réalisé uniquement si le résultat du calcul fait par l’ALU est inférieur ou égal à 0.

Avec ces six instructions, il est possible de supporter les instructions conditionnelles et les boucles avec le minuscule langage d’assemblage. Commençons par les instructions conditionnelles. Supposons que l’on veuille mettre dans la variable y la valeur absolue de la variable x. En python, une première approche pourrait être celle du programme ci-dessous.

y=x
if (x<0):
  y=-x
# y contient abs(x)
z=0

Une première solution pour traduire ces trois lignes de python est de les traduire le plus littéralement possible.

Tableau 16 Calcul de la valeur absolue en minuscule assembleur

adresse

instruction

41

@22 // x

42

D=M

43

@23 // y

44

MD=D

45

@49

46

D;JLT

47

@51

48

0;JMP

49

@23

50

M=-D

51

@24 // z

52

M=0

Vous pouvez télécharger cet exemple depuis asm/ex11a.asm.

Il est intéressant d’analyser l’exécution du programme du Tableau 16 pas à pas. Les instructions aux adresses 41 et 42 placent la valeur de la variable x dans le registre D. Les deux instructions suivantes sauvent le contenu de ce registre dans la variable y. L’instruction à l’adresse 45 charge l’adresse 49 dans le registre A. Cette adresse est celle de la première instruction correspondant au corps du if. L’instruction suivante va elle comparer le contenu du registre D avec 0. Si le registre D est strictement négatif, alors l’adresse se trouvant dans le registre A, c’est-à-dire 49 est placée dans le compteur de programme. Dans ce cas, le programme exécutera le corps de l’instruction conditionnelle. Si par contre le contenu du registre D est positif ou nul, nous ne devons pas exécuter le corps de la boucle, mais directement passer à l’instruction qui initialise la variable z à partir de l’adresse 51. C’est le rôle de l’instruction de saut inconditionnel aux adresses 47 et 48. L’instruction à l’adresse 49 est celle du corps de l’instruction conditionnelle. A la fin de son exécution on peut exécuter l’instruction qui suit l’instruction conditionnelle.

En y réfléchissant un peu, on peut réduire le nombre d’instructions conditionnelles dans ce programme en utilisant une instruction JGE (Tableau 17).

Tableau 17 Calcul de la valeur absolue en minuscule assembleur

adresse

instruction

41

@22 // x

42

D=M

43

@23 // y

44

M=D

45

@49

46

D;JGE

47

@23

48

M=-D

49

…

Vous pouvez télécharger cet exemple depuis asm/ex11.asm.

Il est intéressant d’analyser l’exécution du programme du Tableau 17 pas à pas. Les instructions aux adresses 41 et 42 placent la valeur de la variable x dans le registre D. Les deux instructions suivantes sauvent le contenu de ce registre dans la variable y. L’instruction à l’adresse 45 charge l’adresse 49 dans le registre A. L’instruction suivante va elle comparer le contenu du registre D avec 0. Si le registre D est positif ou nul, alors l’adresse se trouvant dans le registre A, c’est-à-dire 49 est placée dans le compteur de programme. Sinon, les instructions aux adresses 47 et 48 sont exécutées. Par rapport au code python, on remarque que l’on prend comme condition pour l’instruction assembleur l’inverse de la condition du code python. En effet, la condition de l’instruction conditionnelle en python doit être vérifiée pour que l’instruction y=-x soit exécutée. En assembleur, on place la cible du saut après l’exécution des instructions qui se trouvent dans le corps du if en python. Analysons une seconde variante du calcul de la valeur absolue.

if (x>0):
  y=x
else:
  y=-x
# y contient abs(x)

Une première approche pour traduire ce code python en minuscule assembleur serait de procéder comme dans la Tableau 18.

Tableau 18 Essai de calcul de la valeur absolue en minuscule assembleur

adresse

instruction

41

@22 // x

42

D=M

43

@47

44

D;JLE

45

@23 // y

46

M=D

47

@23 // y

48

M=-D

49

…

Vous pouvez télécharger cet exemple depuis asm/ex12.asm.

Malheureusement, cette solution est incorrecte car elle place toujours la valeur de la variable -x dans la variable y quel que soit son signe. Lorsque x est négatif, l’exécution passe directement à l’instruction se trouvant à l’adresse 47 et sauve la valeur de -x dans la variable y. Cependant, si x est positif, après avoir copié x dans la variable y (instructions aux adresses 45 et 46), le minuscule processeur exécute les instructions aux adresses 47 et 48 et sauve donc la valeur de -x dans la variable y. On peut éviter ce problème en utilisant un saut inconditionnel après le corps du if ... (Tableau 19).

Tableau 19 Calcul de la valeur absolue en minuscule assembleur

adresse

instruction

41

@22 // x

42

D=M

43

@47

44

D;JLE

45

@23 // y

46

M=D

47

@51

48

0;JMP

49

@23 // y

50

M=-D

51

…

Vous pouvez télécharger cet exemple depuis asm/ex12b.asm.

Dans l’exemple de la Tableau 19, le saut inconditionnel des instructions aux adresses 47 et 48 garantit que les instructions des adresses 49 et 50 ne seront pas exécutées lorsque x est positif.

Un approche similaire peut être utilisée pour implémenter d’autres instructions conditionnelles. Le tout est de ramener toute condition à une comparaison avec la valeur 0 ou à une comparaison de signe. Ainsi, pour comparer si deux variables contiennent la même valeur, il suffira de calculer une soustraction et ensuite de vérifier si le résultat est nul. Il en va de même pour vérifier si deux variables contiennent des valeurs différentes.

Pour les conditions plus complexes, il faut parfois réécrire l’instruction conditionnelle. Prenons deux exemples en python pour illustrer cette réécriture.

if (a>0) AND (b<1):
   x=2

Dans ce cas, on peut réécrire l’instruction conditionnelle sous la forme :

if (a>0) :
  if (b<1) :
    x=2

Ces deux instructions conditionnelles imbriquées peuvent facilement s’implémenter avec les instructions de saut conditionnel que nous avons présenté. Il en va de même pour une disjonction logique. L’instruction ci-dessous :

if (a>0) OR (b<1):
   x=3

peut se réécrire de la façon suivante pour supprimer la disjonction logique.

if (a>0) :
  x=3
else :
  if (b<1) :
      x=2

A nouveau, les deux instructions conditionnelles ci-dessous peuvent facilement s’implémenter avec les instructions conditionnelles de notre minuscule langage d’assemblage.

Lorsque l’on utilise le langage d’assemblage, il peut être fastidieux de devoir indiquer les valeurs numériques des adresses des variables ainsi que des adresses des sauts. Heureusement, l’assembleur du minuscule processeur vous permet d’utiliser des symboles qui correspondent à ces adresses. Avec ces symboles, notre exemple du calcul de la valeur absolue (Tableau 19) peut s’écrire comme suit :

// valeur absolue
   @x    // variable, adresse choisie par l'assembleur
   D=M
   @SUITE // adresse calculée par l'assembleur
   D;JLE
   @y    // variable, adresse choisie par l'assembleur
   M=D
   @SUITE
   0;JMP
   @y
   M=-D
(SUITE)
//  ...

Vous pouvez télécharger cet exemple depuis asm/ex13.asm.

Dans ce code, l’assembleur construit automatiquement la table des symboles permettant de sauver les variables x et y. Il détermine aussi l’adresse en mémoire de l’instruction qui correspond à l’étiquette (SUITE) et remplace cette étiquette par l’adresse correspondante dans le code. Cela simplifie l’écriture de programmes en minuscule assembleur.

Exercices

  1. Convertissez en minuscule assembleur l’instruction conditionnelle suivante :

    if(x!=y):
  a=x+y
else:
  a=x-y

  2. Convertissez en minuscule assembleur le code python ci-dessous :

    if(x>a) and (x<b) :
  i=1
else:
  i=0

  3. Convertissez en minuscule assembleur le code python ci-dessous :

    if(x==a) or (x>b) :
  y=a
else:
  y=-1

Les boucles

Après les opérations arithmétiques et logiques et les instructions conditionnelles, il nous reste à voir comment supporter les boucles. Python supporte deux types principaux de boucles :

  • les boucles while

  • les boucles for

Les boucles while sont les boucles les plus générales. Un boucle for est généralement une boucle d’un type particulier qui est écrite de façon compacte. Nous nous focaliserons sur les boucles while dans cette section. Une boucle while comprend toujours une condition qui est une expression booléenne et un corps comprenant une ou plusieurs instructions à exécuter. Nous avons déjà vu que la boucle infinie

while True:
  x=x+1

pouvait être traduite dans notre minuscule assembleur par les instructions reprises en Tableau 20.

Tableau 20 Une boucle infinie

adresse

instruction

71

@22

72

M=M+1

73

@71

74

0;JMP

Vous pouvez télécharger cet exemple depuis asm/ex14.asm.

Nous pouvons nous inspirer de cette approche pour traduire une boucle while en une séquence d’instructions en minuscule assembleur. Pour cela, notre programme doit :

  1. Évaluer la valeur de la condition

  2. Si la condition s’évalue à True, exécuter le corps de la boucle puis revenir au point 1

  3. Sinon, passer à l’exécution des instructions placées juste après le corps de la boucle

Pour illustrer cette traduction, considérons la boucle ci-dessous. Après l’exécution de cette boucle, la variable x contient la valeur 512.

x=1
n=1
while (n<10) :
  x=x+x
  n=n+1

Le code assembleur correspondant est présenté ci-dessous. L’étiquette (DEBUT) correspond à la première instruction. Nous initialisons ensuite les variables x et n à la valeur 1 dans les deux mots de mémoire que l’assembleur leur a réservé. L’étiquette (DBOUCLE) correspond à l’adresse de la première instruction de notre boucle. Les quatre instructions qui suivent placent dans le registre D le résultat de \(n-10\). Cela nous permet ensuite de comparer cette valeur avec 0. Si \(n-10 \ge 0\), alors la condition de notre boucle n’est pas vérifiée et nous devons en sortir. C’est le rôle de l’instruction JGE qui placera l’adresse de l’étiquette (FBOUCLE) dans le compteur de programme. Sinon, les six instructions suivantes permettent de placer x+x dans la variable x et ensuite d’incrémenter la variable n. Les deux dernières instructions permettent de revenir à l’adresse de l’étiquette (DBOUCLE) pour faire l’itération suivante dans la boucle.

(DEBUT)
       @x
       M=1
       @n
       M=1
(DBOUCLE)
       @10
       D=A
       @n
       D=M-D
       @FBOUCLE
       D;JGE
       @x
       D=M
       @x
       M=D+M
       @n
       M=M+1
       @DBOUCLE
       0;JMP
(FBOUCLE)

Le programme en minuscule assembleur est téléchargeable via asm/boucle.asm.

Exercices

  1. Écrivez un programme en assembleur pour calculer la somme des n premiers naturels.

  2. Le reste de la division euclidienne entre deux naturels a % b peut s’obtenir en faisant une série de soustractions. En python, cela peut s’écrire comme suit

    # place dans r le reste de la division euclidienne a/b
r=a
while(r>=b):
   r=r-b

Convertissez ce programme python en une suite d’instructions en minuscule assembleur.

Python, comme d’autres langages de programmation, support les mode clés break et continue qui peuvent être utilisé à l’intérieur de boucles. Prenons comme exemple la boucle ci-dessous.

x=9
while(x<a):
   x=x+b
   if(x>c):
     x=c
     break

Ce fragment de code en python peut être traduit en minuscule assembleur par les instructions ci-dessous (téléchargeable via asm/boucle-break.asm). La traduction en assembleur de ce fragment de code montre que l’instruction break est traduite comme un saut inconditionnel qui permet de sortir de la boucle.

	@9
	D=A
        @x
        M=D
   (DBOUCLE)
	@a
	D=M
	@x
	D=M-D
	@FBOUCLE
	D;JGE      // while(x<a)
	@b
	D=M
	@x
	M=D+M
	@x	   // x=x+b	
	D=M
	@c
	D=D-M
	@FINIF
	D;JLE      // if(x>c)
	@c
	D=M     
	@x
	M=D        // x=c  
	@FBOUCLE   
	0;JMP      // break
   (FINIF)	
	@DBOUCLE  
	0;JMP
   (FBOUCLE)

Python supporte aussi l’instruction continue qui permet de continuer l’exécution de la boucle sans exécuter les instructions se trouvant après cette instruction. La code ci-dessous est un exemple de l’utilisation de continue en python.

x=7
while(x<a):
   if(x<c):
     x=x+1
     continue
   x=x+b

A nouveau, la traduction de ce code en minuscule assembleur fait appel à un saut inconditionnel pour supporter l’instruction continue, mais cette fois-ci vers l’étiquette (DBOUCLE) qui correspond au début de la boucle.

	@7
	D=A
        @x
        M=D
   (DBOUCLE)
	@a
	D=M
	@x
	D=M-D
	@FBOUCLE
	D;JGE     // while(x<a)
	@x		
	D=M
	@c
	D=D-M     
	@SUITE
	0;JGE     // if (x<c)
	@x
	M=M+1     // x=x+1
	@DBOUCLE
	D;JMP
   (SUITE)	
	@b
	D=M
	@x
	M=D+M     // x=x+b
	@DBOUCLE  
	0;JMP
   (FBOUCLE)

Ce programme en minuscule assembleur est téléchargeable via asm/boucle-continue.asm.

Tests de programmes en langage d’assemblage

Le langage d’assemblage est un langage de très bas niveau car il manipule directement la mémoire et les registres du minuscule processeur. Même si il ne supporte que deux types d’instructions, il est suffisamment expressif pour permettre des logiciels complexes. Tout comme pour les langages de programmation de plus haut niveau comme python, il est très important de bien tester et de vérifier le bon fonctionnement des programmes écrits en langage d’assemblage.

Pour ces tests, le livre de référence propose un simulateur du minuscule processeur qui peut s’utiliser de deux façons :

  • exécution pas à pas d’un programme via l’interface graphique

  • exécution « en batch » d’un programme et d’une suite de tests qui y est associée

L’exécution pas à pas est très pratique pour bien comprendre le fonctionnement d’un programme en langage d’assemblage ou détecter des erreurs durant son développement. L’interface graphique (Fig. 110) du simulateur est assez intuitive.

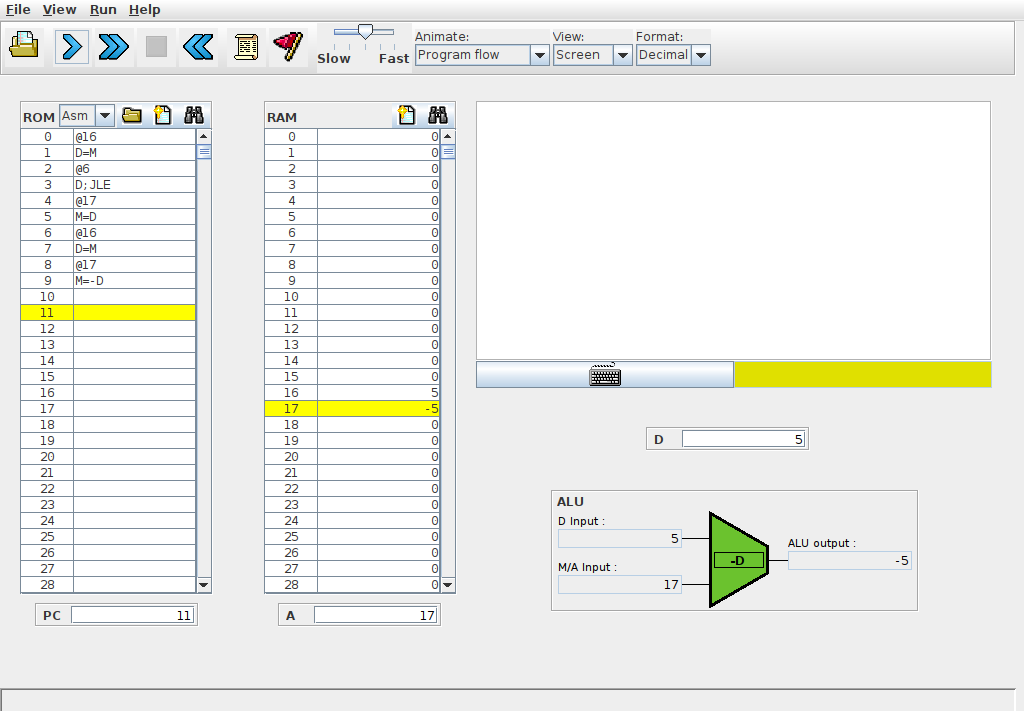
_images/cpu-sim.png

Fig. 110 Simulateur interactif du minuscule processeur

Le menu File permet de charger un programme en langage d’assemblage. Celui-ci peut avoir été écrit avec un éditeur de texte ou être du code machine qui a été produit par l’assembleur fourni avec le livre. Lorsque le simulateur du minuscule CPU charge un programme en langage d’assemblage, il vérifie d’abord sa syntaxe et affiche un message d’erreur en rouge en cas de problème. Ces messages d’erreur ne sont pas toujours explicites. Quand un tel message apparaît, il peut être utile de charger le programme dans l’assembleur de façon à vérifier sa syntaxe et le corriger si nécessaire.

Le programme chargé apparaît dans le tableau de gauche qui représente la ROM du minuscule ordinateur. Il est possible de modifier les instructions se trouvant dans ce tableau, mais pas de sauver la ROM modifiée dans un fichier. La mémoire RAM contenant les données est représentée par le second tableau. La partie droite de la fenêtre du simulateur représente l’écran graphique et le clavier.

Les trois registres du minuscule ordinateur sont représentés par des boites. La première est le PC qui se trouve en bas à gauche. Le registre A qui contient l’adresse en RAM à laquelle il faut lire les données se trouve en dessous de la RAM. Enfin, la partie droite de la fenêtre représente l’ALU avec le contenu du registre D juste au-dessus.

Il est possible d’exécuter un programme en minuscule langage d’assemblage de trois façons différentes. La première est l’exécution pas à pas. En cliquant sur la flèche bleue simple, on simule un cycle d’horloge et donc l’exécution d’une instruction. Cela permet d’observer l’exécution de petits programmes et l’effet de chaque instruction sur les différents registres et la mémoire. Cette exécution pas à pas reste fastidieuse pour de grands programmes.

La seconde méthode pour exécuter un programme est de définir des conditions d’arrêt ( breakpoints en anglais). Ces conditions permettent de spécifier quand l’exécution du programme doit s’arrêter. Ces conditions peuvent être :

  • une valeur du PC

  • un nombre de cycles d’horloge

  • une valeur particulière dans le registre A ou le registre D

  • une valeur stockée à une adresse en mémoire (cela permet de prendre en compte les valeurs des variables stockées en mémoire)

Grâce à ces conditions, il est possible de lancer l’exécution d’un programme et de passer au mode pas à pas dans la région du code qui est la plus intéressante. Plusieurs conditions d’arrêt peuvent être définies. Le simulateur les évalue lorsqu’il exécute chaque instruction et s’arrête dès qu’une condition est vérifiée.

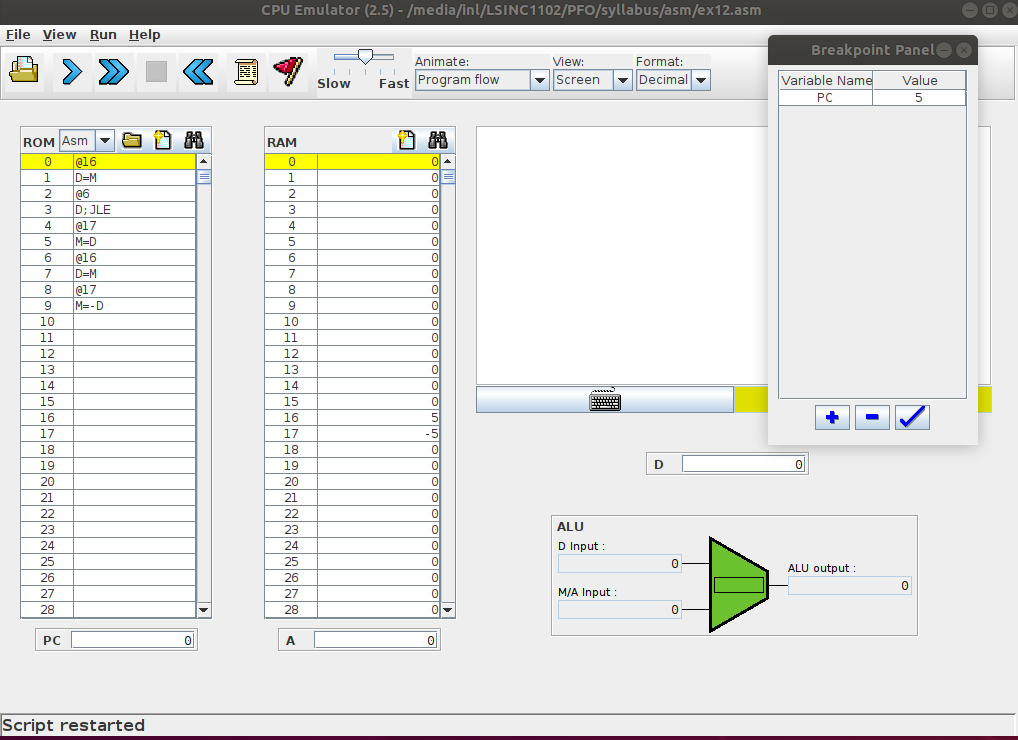
_images/cpu-sim-break.png

Fig. 111 Breakpoints avec le simulateur interactif du minuscule processeur

La troisième méthode et d’écrire un script qui contrôle l’exécution du simulateur. Ces scripts sont un extension de ceux que vous avez déjà utilisé pour les circuits logiques. Ils permettent d’initialiser certaines zones de la mémoire et d’analyser le résultat de l’exécution d’un programme. Il est très utile de construire une script de test avant d’écrire un programme en assembleur.

Pour illustrer l’utilisation de ces scripts, reprenons le programme qui permet de calculer la valeur absolue d’un nombre entier. Nous avons vu précédemment que le code repris ci-dessous ne fonctionnait pas correctement

   @x  
   D=M
   @LABEL
   D;JLE	
   @y  
   M=D
(LABEL)	
   @x
   D=M
   @y  
   M=-D

Ce programme a comme entrée un entier qui est stocké à l’adresse 16 (@x)en mémoire RAM. La valeur absolue calculée se trouve à l’adresse 17 (@y). La première étape pour tester un tel programme est de définir les résultats attendus pour chaque exécution du programme. A la fin de chaque exécution, nous devons vérifier les valeurs se trouvant en mémoire aux adresses 16 et 17.

| RAM[16]  | RAM[17]  | 
|       0  |       0  | 
|       1  |       1  | 
|       7  |       7  |
|      -3  |       3  |
|      -1  |       1  |

Ce fichier est téléchargeable via asm/abs.cmp.

Les cinq lignes du fichier ci-dessus correspondent aux différents cas d’utilisation de notre programme de calcul de la valeur absolue. Un programme qui passe ces cinq tests devrait calculer la valeur absolue correctement.

Nous pouvons maintenant écrire notre script de test. Celui-ci contient d’abord une initialisation qui déclare le nom du fichier en langage machine à exécuter (abs.hack dans notre exemple), le fichier de sortie (abs.out dans notre exemple) et le format des données de sortie.

Ensuite, nous pouvons définir chaque test en initialisant le registre PC à 0 et en plaçant les valeurs souhaitées en RAM. La commande ticktock permet de faire passer un cycle d’horloge et donc d’exécuter une instruction. La commande repeat x { ... } répète x fois les instructions se trouvant dans le bloc { ... }. Enfin, la commande ouput sauve dans le fichier de sortie les données définies dans la commande output-list. Un exemple complet est repris ci-dessous.

// Script de test du programme de calcul de la valeur absolue
load abs.hack,         // le fichier contenant le programme en langage machine
output-file abs.out,   // le fichier de sortie
//compare-to abs.cmp,    // les résultats attendus
output-list RAM[16]%D2.6.2 RAM[17]%D2.6.2;  // les deux valeurs

// premier test, abs(0)=0
set PC 0,      // démarrage du minuscule processeur
set RAM[16] 0, // valeur d'entrée
set RAM[17] 0; // initialisation de la mémoire 
repeat 20 {    // vingt cycles d'horloge devraient suffire
  ticktock;
}
output; // Sauvegarde dans le fichier sortie

// deuxième test, abs(1)=1
set PC 0,      
set RAM[16] 1, 
set RAM[17] 1; 
repeat 20 {   
  ticktock;
}
output; 

// troisième test, abs(7)=7
set PC 0,      
set RAM[16] 7, 
set RAM[17] 7; 
repeat 20 {   
  ticktock;
}
output; 

// quatrième test, abs(-3)=3
set PC 0,      
set RAM[16] -3, 
set RAM[17] 3; 
repeat 20 {   
  ticktock;
}
output; 

// cinquième test, abs(-1)=1

set PC 0,      
set RAM[16] -1, 
set RAM[17] 1; 
repeat 20 {   
  ticktock;
}
output;

Lors de son exécution, le script retourne le résultat de l’exécution de notre programme. Une comparaison avec les valeurs attendues nous indique clairement que notre implémentation est erronée.

| RAM[16]  | RAM[17]  |
|       0  |       0  |
|       1  |      -1  |
|       7  |      -7  |
|      -3  |       3  |
|      -1  |       1  |

Dans le cadre des projets, nous vous encourageons à écrire d’abord le script de test avant d’écrire vos programmes et pas l’inverse. N’hésitez pas à écrire des petits scripts de test pour de petites parties de votre programme afin des les valider une après l’autre.

Langage d’assemblage : compléments

Dans ce chapitre, nous allons d’abord voir comment notre minuscule ordinateur peut interagir avec le monde extérieur (écran et clavier) et ensuite comment manipuler des tableaux et des chaînes de caractères stockés en mémoire.

Entrées-sorties

Un ordinateur doit interagir avec son environnement. Les ordinateurs actuels comprennent de très nombreux dispositifs pour interagir avec les humains et le monde extérieur via des capteurs, clavier, souris, écran, … Le minuscule ordinateur se limite à deux dispositifs: un écran qui est son unique dispositif de sortie et un clavier qui est son unique dispositif d’entrée. Les principes que l’on va présenter pour ces deux dispositifs sont génériques et peuvent s’appliquer à d’autres dispositifs d’entrée ou de sortie. En anglais, on parle généralement de dispositifs d’I/O pour Input/Output.

Commençons par le clavier qui est le dispositif le plus simple. Un clavier peut s’interfacer de différentes façons avec un ordinateur. On peut voir un clavier comme une sorte de matrice dans laquelle chaque touche correspond à une position dans la matrice. Lorsqu’un utilisateur pousse sur une touche, l’élément correspondant de la matrice est mis à une valeur convenue. Si l’utilisateur pousse sur plusieurs touches, les positions correspondantes de la matrice sont modifiées. Cela permet de supporter des claviers avec des touches telles que shift ou ctrl dont la pression modifie le caractères correspondant à une autre touche.

Le minuscule ordinateur prend une approche beaucoup plus simple. Il ne représente pas les touches tapées par l’utilisateur mais retourne directement le mot de 16 bits qui correspond au caractère tapé par l’utilisateur. Il reste cependant à déterminer comment un programme peut accéder à ce caractère. Pour cela, le minuscule ordinateur utilise la technique des entrées/sorties mappées en mémoire (memory-mapped I/O en anglais). Cette technique est à la fois très simple, mais aussi très fréquemment utilisée pour supporter de très nombreux dispositifs d’entrée-sortie.

Le clavier du minuscule ordinateur comprend un registre qui contient le code ASCII du caractère sur lequel l’utilisateur tape actuellement sur le clavier. Si l’utilisateur ne tape pas sur le clavier, celui-ci contient la valeur 0. En outre, le minuscule ordinateur définit les caractères de contrôle repris dans le Tableau 21.

Tableau 21 Caractères de contrôle

Touche

Code ASCII

retour à la ligne

128

backspace

129

flèche gauche

130

flèche haut

131

flèche droite

132

flèche bas

133

home

134

end

135

page up

136

page down

137

insert

138

delete

139

escape

140

f1-f12

141-152

Les concepteurs du minuscule ordinateur ont réservé une adresse mémoire pour ce registre du clavier : l’adresse 24576 (0x6000 en hexadécimal). La mémoire du minuscule ordinateur a été conçue de façon à ce que lorsqu’un programme demande à lire le mot se trouvant à cette adresse, il lit le contenu du registre du clavier.

Le programme ci-dessous présente un exemple simple de lecture de caractères depuis le clavier. Le compteur c compte simplement le nombre de fois qu’une touche a été pressée.

	@c
	M=0
(LOOP)
	@24576 // keyboard 
	D=M
	@LOOP
	D;JEQ
	@c
	M=M+1
	@LOOP
	0;JMP

Ce programme peut être téléchargé via le lien asm/keyb.asm.

Lorsque l’on exécute ce programme en utilisant le simulateur du minuscule CPU, on observe facilement que le compteur n’est incrémenté qu’à condition que la touche soit pressée au moment où le programme lit le mot à l’adresse 24576 en mémoire. Dès que l’utilisateur arrête de pousser sur un touche, ce mot revient à la valeur 0. Cela implique que sur le minuscule ordinateur, il est nécessaire de consulter très régulièrement l’information stockée à cette adresse pour réagir à la pression d’une touche sur le clavier. C’est le rôle notamment du système d’exploitation, mais cela sort du cadre de ce cours.

Cette technique de lecture de données sous la forme d’une boucle qui lit en permanence l’information mappée en mémoire à une adresse donnée s’appelle le polling. Elle a l’avantage d’être très rapide puisqu’il suffit d’attendre le temps d’exécution de quelques instructions pour que la donnée soit disponible dans le programme. Elle est encore utilisée de nos jours lorsqu’il est nécessaire de réagir très rapidement sur certains dispositifs d’entrée. Malheureusement, elle souffre d’un inconvénient majeur. Le processeur doit en permanence exécuter un programme qui consulte les adresses mappées en mémoire pour voir de l’information est disponible. Pour un dispositif tel que le clavier via lequel l’utilisateur pousse sur quelques touches chaque seconde, il n’est pas souhaitable que le processeur consacre une bonne partie de sa puissance de calcul pour simplement vérifier si une touche a été pressée.

Pour éviter ce problème, les ordinateurs actuels supportent aussi les entrées-sorties par interruption. Les détails de cette technique sortent du cadre de ce cours introductif. En simplifiant, l’idée de base des interruptions est la suivante. On ajoute sur le minuscule processeur un signal de contrôle baptisé interruption. Ce signal est connecté aux dispositifs d’entrée-sortie. Lorsqu’une nouvelle information est disponible sur un dispositif, celui-ci met le signal d’interruption à 1. Après l’exécution de chaque instruction, le processeur vérifie la valeur du signal d’interruption. Si celui-ci vaut 0, il continue l’exécution du programme en cours. Par contre, si le signal d’interruption vaut 1, le processeur sauvegarde la valeur actuelle du PC et passe à l’exécution d’un programme spécial dédié au traitement des interruptions. Ce programme, qui fait généralement partie du système d’exploitation, consulte les différents dispositifs d’entrée-sortie pour voir quelle information est disponible et la traite rapidement. Ensuite, il récupère l’ancienne valeur du PC et relance automatiquement l’exécution du programme qui avait été interrompu par l’interruption à l’adresse de l’instruction où il s’était arrêté. Un programme de traitement des interruptions doit être écrit avec précautions car il ne peut perturber le programme qui s’exécutait au moment de l’interruption.

Nous pouvons maintenant étudier l’écran comme exemple de dispositif de sortie. Tout comme pour le clavier, celui-ci utilise la technique des entrées-sorties mappées en mémoire. L’écran du minuscule ordinateur est un écran rectangulaire en noir et blanc de 256 pixels de haut et 512 pixels de large. Il est représenté par un bloc de 8192 adresses en mémoire à partir de l’adresse 16384 (0x4000 en hexadécimal) en RAM. La valeur de chaque pixel est encodé sur un bit (1 pour un pixel noir et 0 pour un pixel blanc). Voici un premier exemple qui remplit l’écran en noir en parcourant tous les pixels et toute la mémoire correspondant à l’écran.

	@pixel
	M=-1
	@16384   // screen
	D=A
	@pos
	M=D
	@8192
	D=A
	@count
	M=D
(LOOP)
	@pixel
	D=M
	@pos
	A=M
	M=D
	@pos
	M=M+1
	@count
	MD=M-1
	@LOOP
	D;JGT

Ce programme peut être téléchargé via le lien asm/screen.asm.

En écrivant une donnée en mémoire, on peut donc afficher un pixel à l’écran. L’adresse 16384 correspond au pixel se trouvant dans le coin supérieur gauche de l’écran. Si on attribue les coordonnées (0,0) à ce point et que l’axe des ordonnées (y) est croissant vers le bas tandis que celui des abscisses (x) est croissant vers la droite, alors dans ce repère, le pixel en position (x,y) corresponde à l’adresse mémoire \(16384 + y \times 32 + x / 16\) où / est le quotient de la division entière. Il y a donc 16 pixels qui sont encodés dans le même mot de 16 bits en mémoire. Dans celui-ci, le bit \(x \% 16\) est celui qui correspond à notre pixel.

En utilisant cette représentation binaire des pixels, il est possible de dessiner des caractères et autres formes géométriques à l’écran. Commençons par écrire un petit caractère que vous reconnaîtrez rapidement.

\def\pixels{ {0,0,0,0,0,0,0,0}, {0,0,1,0,0,1,0,0}, {0,0,0,0,0,0,0,0}, {0,0,0,0,0,0,0,0}, {0,1,0,0,0,0,1,0}, {0,0,1,0,0,1,0,0}, {0,0,1,1,1,1,0,0}, {0,0,0,0,0,0,0,0},% } \definecolor{pixel 1}{HTML}{000000} \definecolor{pixel 0}{HTML}{FFFFFF} \foreach \line [count=\y] in \pixels { \foreach \pix [count=\x] in \line { \draw[fill=pixel \pix] (\x,-\y) rectangle +(1,1); } }

Fig. 112 Un caractère sous la forme de pixels

Le caractère dessiné en Fig. 112 occupe huit lignes de huit pixels chacune. La première contient l’octet 0. La deuxième l’octet 00100100 en notation binaire. Les troisième et quatrième contiennent également l’octet 0. La cinquième contient l’octet 01000010, la sixième 00100100 et la septième 00111100. La dernière contient à nouveau l’octet 0. Pour afficher ce caractère à l’écran, il faut se souvenir que si un pixel se trouve à l’adresse A, alors le pixel qui se trouve en dessous de lui est à l’adresse A+32 puisque chaque ligne de notre écran comprend 512 pixels qui sont encodés sur 32 mots de 16 bits chacun.

Ce caractère peut être affiché à l’écran en utilisant les instructions suivantes.

	@pos
	M=0
	@20000   // position du caractère l'écran
	D=A
	@pos
	M=D
	@0   // première ligne
	D=A
	@pos
	A=M
	M=D
	@32
	D=A
	@pos
	M=M+D
	@36  // deuxième ligne
	D=A
	@pos
	A=M
	M=D
	@32
	D=A
	@pos
	M=M+D
	@0   // troisième ligne
	D=A
	@pos
	A=M
	M=D
	@32
	D=A
	@pos
	M=M+D
	@0   // quatrième ligne
	D=A
	@pos
	A=M
	M=D
	@32
	D=A
	@pos
	M=M+D
	@68  // cinquième ligne
	D=A
	@pos
	A=M
	M=D
	@32
	D=A
	@pos
	M=M+D
	@36  // sixième ligne
	D=A
	@pos
	A=M
	M=D
	@32
	D=A
	@pos
	M=M+D
	@60  // septième ligne
	D=A
	@pos
	A=M
	M=D
	@32
	D=A
	@pos
	M=M+D
	@0   // huitième ligne
	D=A
	@pos
	A=M
	M=D
	@32
	D=A
	@pos
	M=M+D

Ce programme peut être téléchargé via le lien asm/screen.asm.

Notre dernier exemple portera sur le dessin d’un rectangle. Pour simplifier ce dessin, nous supposerons que la longueur de notre rectangle est un multiple de 32 pixels. Notre rectangle sera défini par trois paramètres :

  • l’adresse mémoire à laquelle il débute

  • sa longueur (un multiple de 32 pixels)

  • sa hauteur (en pixels)

Ce programme comprendra deux boucles imbriquées. La première va permettre d’afficher une ligne horizontale noire de l’adresse A à l’adresse A+long où long est la longueur du rectangle. Cette boucle se trouvera à l’intérieur d’une boucle qui incrémente la position verticale de la ligne de façon à dessiner les haut lignes de notre rectangle.

// rectangle
	@noir
	M=-1
	@17996   // coin supérieur gauche
	D=A
	@coin
	M=D
	@16      // longueur
	D=A
	@long
	M=D
	@12
	D=A
	@haut   // hauteur
	M=D
	@x
	M=0
	@y
	M=0
	@coin
	D=M
	@addr
	M=D
(BOUCLEH)
	@addr
	D=M
	@addrx
	M=D
	@long
	D=M
	@countx
	M=D
(BOUCLEL)
	@noir
	D=M
	@addrx
	A=M
	M=D
	@addrx
	M=M+1
	@countx
	MD=M-1
	@BOUCLEL
	D;JGT
	@32
	D=A
	@addr
	M=M+D
	@haut
	MD=M-1
	@BOUCLEH
	D;JGT