Langage d’assemblage¶
Nous pouvons commencer à programmer un micro-processeur qui est capable d’exécuter de petits programmes. Ce micro-processeur répond à ce que l’on appelle l”architecture de Von Neumann.
Cette architecture est composée d’un processeur (CPU en anglais) ou unité de calcul et d’une mémoire. Le processeur est un circuit électronique qui est capable d’effectuer de nombreuses tâches :
lire de l’information en mémoire
écrire de l’information en mémoire
réaliser des calculs
L’architecture des ordinateurs est basée sur l’architecture dite de Von Neumann. Suivant cette architecture, un ordinateur est composé d’un processeur qui exécute un programme se trouvant en mémoire. Ce programme manipule des données qui sont aussi stockées en mémoire.
Dans un ordinateur, toutes les données et les programmes sont représentés sous la forme de séquences de bits. Pour exécuter un programme, le microprocesseur doit charger les séquences de bits qui correspondent aux instructions depuis la mémoire ainsi que les données qui y sont associées. Le programme est découpé en de très nombreuses instructions très simples, beaucoup plus simples que celles que l’on trouve dans un langage de programmation comme python. Chaque microprocesseur est caractérisé par l’ensemble des instructions qu’il peut exécuter. Les premiers microprocesseurs supportaient quelques dizaines d’instructions différentes. Les processeurs récents en supportent beaucoup plus.
Même si dans l’ordinateur chaque instruction à exécuter est représentée sous la forme d’une séquence de bits, ces séquences sont peu pratiques pour les informaticiens et informaticiennes qui doivent les utiliser pour écrire des programmes. Pour écrire de tels programmes, il est préférable de passer par le langage d’assemblage. Un langage d’assemblage est la liste de toutes les instructions simples qui sont supportées par un microprocesseur donné. Chaque microprocesseur dispose de son langage d’assemblage.
Dans ce syllabus, nous nous concentrons sur un langage d’assemblage simple qui ne correspond pas à un ordinateur réel, mais contient les instructions que l’on retrouve dans la plupart des langages d’assemblage. Son avantage principal est qu’il est très facile d’exécuter des programmes écrits dans ce langage en utilisant le simulateur disponible en ligne. Ce simulateur est utilisable depuis n’importe quel navigateur web.
Notre simulateur¶
Dans le cadre de ce syllabus, nous utilisons simulateur de microprocesseur développé initialement par Marco Schweighauser et amélioré par Nikita Tyunyayev. Cette première partie du syllabus vous permettre de comprendre les principes de base de la programmation d’un microprocesseur simple en assembleur. Ce simulateur est accessible en ligne depuis n’importe quel navigateur web via http://asm.info.ucl.ac.be . La Fig. 2 présente l’interface graphique de notre simulateur.
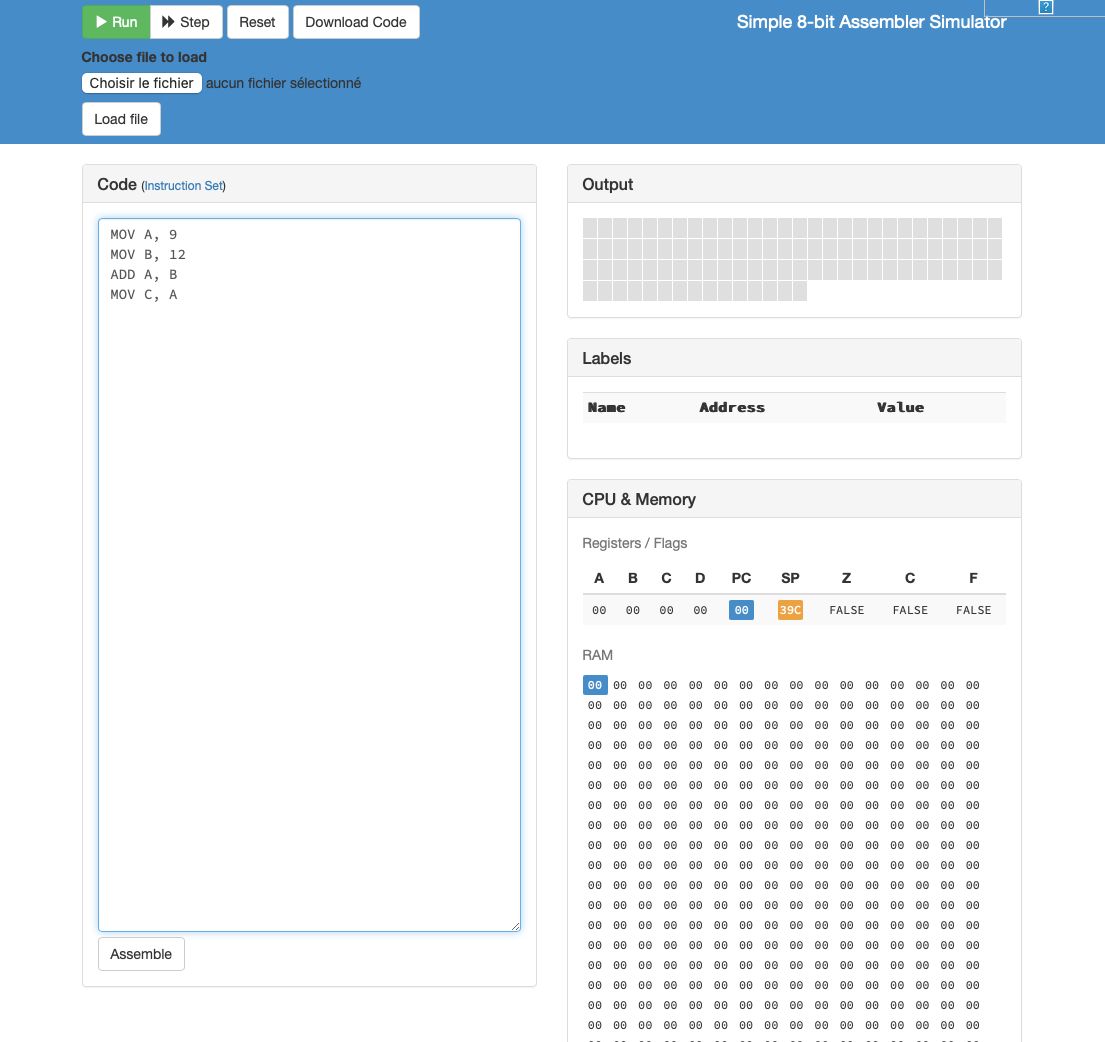
Fig. 2 Capture d’écran du simulateur de processeur¶
Notre simulateur comprend plusieurs boutons en haut de l’écran:
Runpour exécuter l’ensemble du programme pas à pas
Steppour exécuter l’instruction suivante et s’arrêter
Resetpour revenir au début de l’exécution du programme
Download Codepour télécharger sur votre ordinateur le programme chargé sur le simulateur
Choisir le fichierpour sélectionner un fichier sur votre ordinateur
Load filepour charger le fichier sélectionné depuis votre ordinateur vers le simulateur
La grande boîte baptisée Code comprend le code en assembleur à exécuter. La boîte baptisée Output est un écran simplifié que vous pourrez utiliser pour afficher quelques caractères. La boîte CPU & Memory contient d’abord les valeurs des données stockées dans les registres et les drapeaux du processeur. La partie dénommée RAM représente le contenu de la mémoire. Les informations se trouvant dans les registres et la mémoire sont représentées en notation hexadécimale.
Un assembleur simple¶
Tout langage d’assemblage dépend des caractéristiques matérielles du microprocesseur qui supporte ses instructions. Notre processeur contient quatre registres que vous pouvez utiliser
pour stocker des données. Ils sont identifiés par les lettres A,
B, C et D. Chacun de ces registres peut stocker un bloc de
16 bits de données. Comme dans tout stockage binaire de l’information,
c’est au programmeur de décider ce que représente un bloc de bits. Il
peut s’agir d’un caractère, d’un nombre ou de tout autre type
d’information.
Notre ordinateur comprend aussi une mémoire RAM (ou index:Random Access Memory) qui permet de stocker des données et des instructions. Toutes les informations stockées dans la RAM sont sous forme binaire. Tout comme pour les registres, c’est au programmeur de décider si une information se trouvant en mémoire représente un caractère, un nombre ou une instruction.
Notre processeur simple supporte quelques dizaines d’instructions que
nous allons découvrir petit à petit. La première instruction est
baptisée MOV. L’instruction MOV prend deux arguments:
une destination
une source
La syntaxe de base de cette instruction est :
MOV dest, src. La destination est un identifiant de registre (A,
B, C ou D) et la source peut être un identifiant de
registre ou une constante. Cette constante peut être spécifiée en
notation binaire, décimale, octale ou hexadécimale. Lorsque l’on
spécifie une constante, c’est généralement la notation décimale qui
est utilisée, mais parfois il est intéressant d’utiliser une des
autres notations, notamment lorsque l’on veut spécifier une séquence de bits spécifique.
L’instruction MOV permet de placer un bloc de 16 bits dans
un registre ou de déplacer un bloc de 16 bits d’un registre à l’autre.
Dans l’assembleur que nous utilisons, chaque instruction est
représenté par un mot clé en majuscules suivi de ses arguments sur une
ligne. Le caractère ; est utilisé pour marquer le début d’un
commentaire. Une ligne qui débute par le point virgule n’est donc
pas considérée comme une instruction.
Il en va de même pour tous les caractères qui
suivent le point virgule sur une ligne quelconque.
Nous pouvons maintenant exécuter notre première séquence d’instructions. Notre microprocesseur va d’abord exécuter la première instruction. Il exécutera ensuite la deuxième et enfin la troisième.
1 2 3 | MOV A,1 MOV B,2 MOV A,B |
Dans l’exemple ci-dessus, la première ligne place la représentation
binaire du nombre naturel 1, c’est-à-dire 000000000000001
dans le registre A. La deuxième ligne contient l’instruction qui
permet de placer la représentation binaire du nombre naturel 2 dans le
registre B. La troisième instruction permet elle de copier les 16
bits qui se trouvent dans le registre B (c’est-à-dire la valeur
2) dans le registre A. Après l’exécution de ces trois instructions,
les registres A et B contiennent tous les deux la séquence
0000000000000010.
L’instruction MOV, et toutes les instructions de l’assembleur que
nous utilisons, permettent de spécifier leurs arguments numérique en
notation, binaire, décimale, octale et hexadécimale. Dans le cours,
nous privilégierons la notation décimale qui est la plus courante,
mais les autres notations sont parfois utiles lorsque l’on veut
stocker un blocs de 16 bits bien particulier. Les quatre instructions
ci-dessous placent toute la valeur vingt trois dans le registre D.
1 2 3 4 | MOV D, 23d ; en notation décimale MOV D, 0x17 ; en notation hexadécimale MOV D, 0o27 ; en notation octale MOV D, 10111b ; en notation binaire |
Notre processeur peut également réaliser des opérations arithmétiques
sur les données stockées dans ses registres. Les opérations
arithmétiques les plus simples sont INC et DEC. Elles prennent
toutes les deux comme argument un identifiant de
registre. L’instruction INC X incrémente le nombre entier stocké
dans le registre X d’une unité. L’instruction DEC X décrémente
d’une unité la valeur entière stockée dans le registre X.
A titre d’exemple, considérons la séquence d’instructions suivante.
1 2 3 4 5 6 7 8 9 10 11 12 | ; première solution MOV A, 7 ; deuxième solution MOV B, 6 INC B ; troisième solution MOV C, 8 DEC C ; quatrième solution MOV D, 7 DEC D INC D |
Après l’exécution de ces instructions, les quatre registres de notre
processeur contiennent tous la valeur entière 7. La première
ligne est, évidemment, la meilleure solution pour placer cette valeur
dans le registre A, mais les autres aboutissent au même résultat.
Notre processeur peut aussi additionner et soustraire les valeurs
entières stockées dans des registres. L’instruction ADD prend
deux arguments. Le premier est le registre qui est la destination du
résultat. Le second est un registre ou une constante. Cette
instruction calcule la somme entre ses deux arguments et place le
résultat dans le premier argument. L’instruction SUB prend
également deux arguments. Elle stocke dans son premier argument
le résultat de l’opération arg1 - arg2.
MOV A, 7
MOV B, 3
ADD A, B
La séquence d’instructions ci-dessus place dans le registre A la
somme entre la valeur stockée dans ce registre et celle se trouvant
dans le registre B, c’est-à-dire la valeur 10.
MOV A, 7
MOV B, 3
SUB A, B
La séquence d’instruction ci-dessus place dans le registre A le
résultat de l’opération 7 - 3, c’est-à-dire la valeur 4.
Il est intéressant de noter que comme l’instruction ADD ne prend
que deux arguments, il n’est pas possible, en une seule instruction,
de calculer la somme entre deux registres et de la placer dans un
troisième. Cela nécessite deux instructions comme dans la séquence
ci-dessous qui place dans le registre C la somme entre les valeurs
stockées dans les registres A et B.
MOV A, 9
MOV B, 12
ADD A, B
MOV C, A
Il est important de noter qu’après exécution de la séquence
d’instructions ci-dessus, la valeur qui était stockée dans le registre
A est perdue. Si cette valeur était importante pour la suite du
programme, alors il est préférable d’utiliser la séquence
d’instructions qui suit qui elle utilise le registre C comme
mémoire intermédiaire.
MOV A, 9
MOV B, 12
MOV C, A
ADD C, B
Notre microprocesseur est aussi capable de réaliser des opérations
de multiplication et de division. Cependant, ces opérations, qui sont
nettement plus complexes à implémenter que les additions et soustractions,
ne peuvent que porter sur la valeur se trouvant dans le registre A.
Il est donc nécessaire de d’abord placer la valeur à multiplier ou
diviser dans ce registre avant de pouvoir réaliser l’opération.
En utilisant l’instruction MUL, il est possible de multiplier
une valeur entière stockée dans le registre A par une constante.
MOV A, 9
MUL 3
Après exécution du code ci-dessus, le registre A contient la
valeur décimale 27. Il est aussi possible de multiplier la
valeur entière stockée dans le registre A par la valeur se
trouvant dans un autre registre.
MOV A, 9
MOV B, 2
MUL B
Après exécution des instructions ci-dessus, le registre A
contient la valeur décimale 18. Le registre B contient
lui toujours la valeur 2.
L’instruction DIV s’utilise de façon similaire. Il est
possible de diviser la valeur se trouvant dans le registre A
par une constante entière.
MOV A, 24
DIV 3
Après exécution de ces instructions, le registre A
contient la valeur 8 qui est le quotient de la division
de 24 par 3. Tout comme pour l’instruction
de multiplication, il est possible de diviser la
valeur stockée dans le registre A par une valeur
entière se trouvant dans un autre registre.
MOV A, 35
MOV B, 7
DIV B
Après exécution de ces instructions, le registre A
contient la valeur 5. Il est important de noter
que notre processeur calcule le quotient de la division
entière entre le dividende stocké dans le registre
A et le diviseur qui peut être une constante ou
se trouver dans un autre registre. En python, la
séquence d’instructions ci-dessous permet également
de calculer le quotient de cette division entière.
a=35
b=7
a=a//b
Notre langage d’assemblage ne contient pas d’instruction permettant de calculer le reste d’une division entière. Si vous avez besoin de cette opération, vous devrez la programmer en utilisant les autres instructions du langage.
Une dernière instruction qui nous sera utile par après est l’instruction HLT. Cette instruction permet d’arrêter l’exécution du programme. Il faut pousser sur le bouton Reset du simulateur pour redémarrer le processeur.
Interaction avec la mémoire RAM¶
A côté des instructions de calcul telles que celles qui viennent d’être présentées, notre microprocesseur simple est aussi capable d’interagir avec la mémoire. Il existe plusieurs type de mémoires dans un ordinateur. Les deux plus simples sont les Random Access Memory (RAM) et les Read-Only Memory (ROM).
Comme son nom l’indique, une mémoire ROM est une mémoire dont le contenu ne peut qu’être lu. Le contenu de cette mémoire est écrit lors de la construction de la mémoire et ne peut jamais être modifié. Ces mémoires sont utilisées pour stocker des données ou des programmes qui ne changent jamais, comme par exemple le code qui permet de faire démarrer un ordinateur et de lancer son système d’exploitation. Une mémoire ROM peut se représenter comme dans la Fig. 3.
![[
node distance=0.1cm
]
\node (addr) at (0,0) {\small Addr};
\node (rom) [draw,right =of addr, align=center] {
R\\
O\\
M
};
\node (out) [right =of rom] {\small out};
\draw [->] (addr) -- (rom.west);
\draw [->] (rom.east) -- (out);](../_images/tikz-8ba6907853a3a6823e0752f526736f89c109db0a.png)
Fig. 3 Une mémoire ROM
Une caractéristique important des mémoires de type ROM est que leur contenu est préservé même lorsque la mémoire est mise hors tension. Certaines mémoires de type ROM sont dites programmables car il est possible d’effacer et de modifier leur contenu. C’est le cas par exemple des EPROM (Electrically Programmable ROM) ou des EEPROM (Electrically Erasable and Programmable ROM). La programmation d’un tel circuit se fait en utilisant un dispositif spécialisé qui sort du cadre de ce cours.
Une mémoire ROM peut être vue comme un tableau permettant de stocker des données (dans notre ordinateur des blocs de 16 bits). Chaque élément du tableau est identifié par une adresse. A titre d’exemple, considérons une mémoire ROM qui permet de stocker 4 blocs de 16 bits.
Adresse |
Valeur |
0b11 |
0b1100100100100111 |
0b10 |
0b0000000000000001 |
0b01 |
0b0000000000000000 |
0b00 |
0b1111111111111111 |
La mémoire ROM représentée dans la table Tableau 4
contient quatre blocs de 16 bits. Le microprocesseur peut accéder à
chacun de ces blocs en indiquant à la mémoire l’adresse à laquelle
il est stocké. Ainsi, la donnée stockée à l’adresse 0b01 en mémoire
ROM, que l’on pourrait schématiser par la notation
ROM[0b01], est la valeur 0b0000000000000001 ou 1 en notation
décimale.
Une mémoire ROM utilise un nombre de bits d’adresse qui dépend de sa capacité. Une mémoire permettant de stocker \(2^{n}\) blocs de données utilisera des adresses qui sont stockées sur \(n\) bits. Il faut cependant noter que dans la plupart des ordinateurs, les mémoires sont organisées de façon à associer une adresse à chaque octet ou bloc de 8 bits.
Lorsque l’on doit stocker un bloc de 16 bits dans une mémoire dont l’unité
de stockage est l’octet (8 bits), il faut se mettre d’accord sur la convention
utilisée pour stocker les bits de poids fort et les bits de poids faible.
Considérons la séquence de bits 0b 01000000 00000001. Cette séquence de
bits correspond à la valeur entière 8193. Dans une mémoire dont l’unité
de stockage est l’octet, elle peut être stockée de deux façons différentes.
La première convention, baptisée big-endian stocke l’octet de poids
fort (0b01000000`) à l’adresse la plus petite comme illustré dans la
table Tableau 5. C’est la convention qui est utilisée par
notre assembleur ainsi que par certains ordinateurs actuels. Gardez cette
convention en tête lorsque vous analysez le contenu d’une mémoire.
Adresse |
Valeur |
0b1 |
0b00000001 |
0b0 |
0b01000000 |
L’autre convention, baptisée little-endian, est de stoker les bits de poids fort à l’adresse la plus élevée comme représenté dans Tableau 6. Cette convention est utilisée par certains ordinateurs actuels.
Adresse |
Valeur |
0b1 |
0b01000000 |
0b0 |
0b00000001 |
Une mémoire RAM a une organisation similaire. Chaque zone de mémoire permettant de stocker un octet est identifié par une adresse. Tout comme dans une mémoire ROM, le nombre de bits utilisé pour représenter chaque adresse dépend de la capacité de la mémoire.
Dans une mémoire RAM, outre les entrées relatives aux adresses, il faut aussi avoir une entrée load (parfois appelée read/write) pour déterminer si la mémoire doit lire ou écrire une donnée et une entrée data permettant de charger des données dans la RAM. Le nombre de bits d’adresses dépend uniquement de la capacité de la mémoire. En général, une adresse correspond à un octet stocké en mémoire. L’entrée data quant à elle peut permettre de charger des octets, des mots de 16, 32 bits ou encore plus. La Fig. 4 représente une mémoire RAM de façon schématique.
![[
node distance=0.1cm
]
\node (empty) at (0,0) {};
\node (addr) at (-0.5,-0.5) {\small Addr};
\node (data) at (-0.5,0.5) [text=green] {\small Data};
\node (ram) [draw,right =of empty, align=center] {
R\\
A\\
M
};
\node (load) [above =of ram,text=blue] {\small load};
\node (out) [right =of ram] {\small out};
\draw [->] (addr.east) -- (ram.225);
\draw [->,color=green] (data.east) -- (ram.135);
\draw [->] (ram.east) -- (out);
\draw [->,color=blue] (load) -- (ram.north);](../_images/tikz-172e00e90d1e64b6e934b137cde2ca23944ad0cb.png)
Fig. 4 Une mémoire RAM
Cette mémoire RAM peut être utilisée par notre microprocesseur comme mémoire permettant de stocker à la fois les instructions et les données. Tant les instructions que les données sont stockées sous la forme de séquences de bits. Nous analyserons plus tard comment représenter une instruction comme une séquence de bits. Pour le moment, concentrons-nous sur l’utilisation de la mémoire RAM pour stocker des données qui seront utilisées par nos programmes.
Le langage d’assemblage nous permet de précharger en mémoire RAM des constantes qui pourront ensuite être utilisées dans notre programme. Le mot clé DB permet de stocker en mémoire le mot de 16 bits qui suit le mot-clé.
A titre d’exemple, le code ci-dessous stocke le bloc de 16 bits 0b00000000 0000011 à
l’adresse 0 en mémoire et le bloc 0b00000000 00000111 à l’adresse 2.
DB 3
DB 7
Note
DB n’est pas une instruction
Le mot clé DB n’est pas une instruction du langage d’assemblage, c’est une directive
qui indique à l’assembleur de simplement placer en mémoire la valeur qui suit le mot-clé
DB. Cette valeur peut être une valeur décimale, une valeur binaire ou une valeur
en notation hexadécimale. La Fig. 5 illustre l’utilisation de ce mot-clé DB.
Il est intéressant de regarder le contenu de la mémoire RAM et de le mettre en parallèle avec
les mots-clés DB.
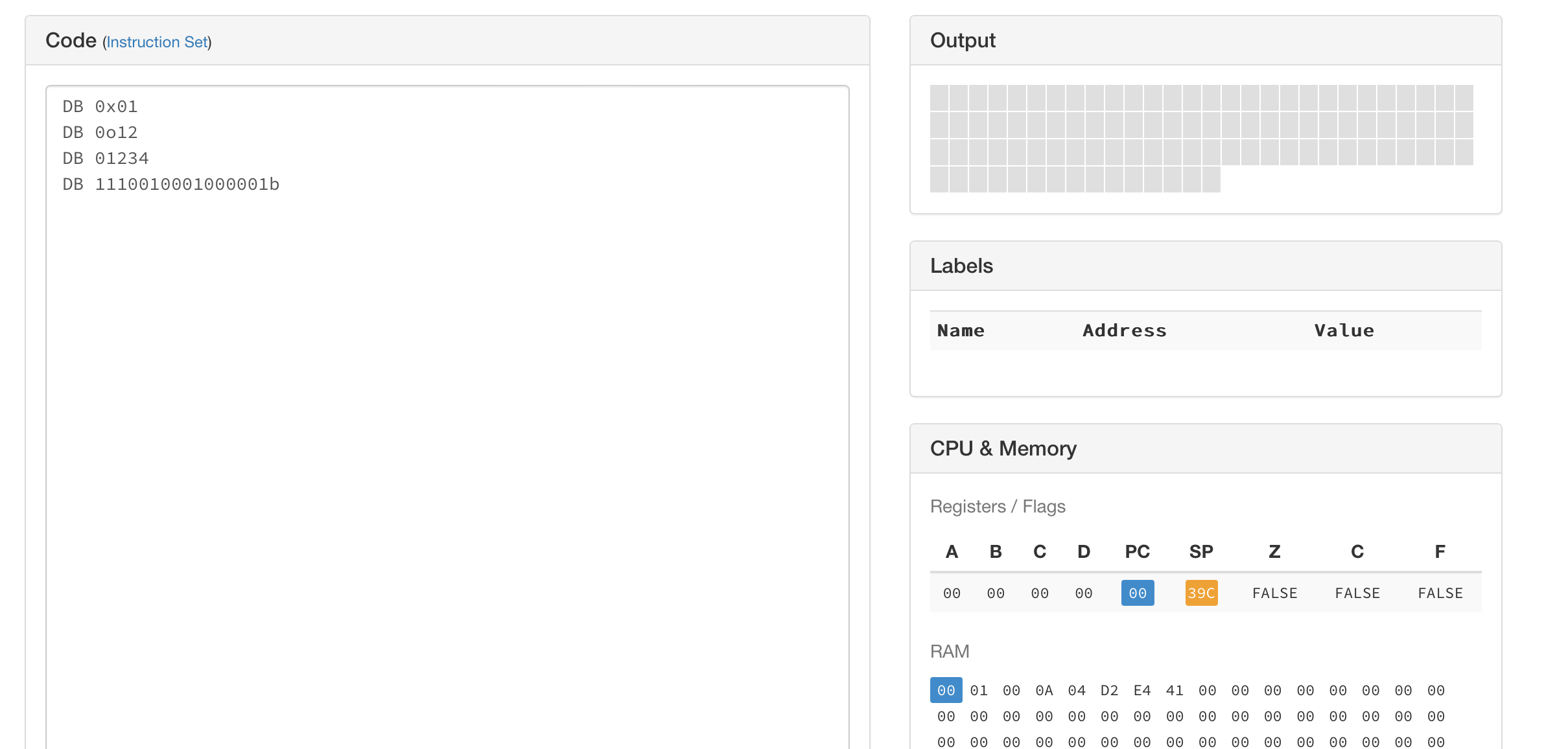
Fig. 5 Exemple d’utilisation du mot-clé DB¶
En pratique, le mot clé DB sera rarement utilisé de cette façon.
Dans un programme, on utilisera ce mot clé pour définir des constantes
ou alors pour fixer la valeur initiale de certaines variables. Dans ces
deux cas d’utilisation, il est important pour le programmeur de pouvoir
connaître l’adresse mémoire correspondant à chacune de ces variables
ou constantes. L’assembleur que nous utilisons permet d’associer une
étiquette (label en anglais) à certaines adresses mémoire. Ces
étiquettes peuvent ensuite être utilisées par les instructions du
programme et elles sont automatiquement traduites par l’assembleur en
l’adresse correspondante. Pour définir une étiquette, il suffit
d’écrire sur une ligne une chaîne de caractères suivie par le caractère
: et ensuite l’instruction en assembleur (souvent DB).
Afin d’illustrer l’utilisation de ces étiquettes, considérons la liste
de mots-clés DB ci-dessous.
zero: DB 0x0000
lln: DB 1348
charleroi: DB 6000
Cette suite de mots-clés nous permet d’initialiser en mémoire trois constantes
et d’associer une étiquette à chacune de ces constantes. La première ligne
place la valeur 0x0000 en mémoire. Cette valeur se trouve à l’adresse
0 et l’assembleur associe l’étiquette zero à cette adresse.
La deuxième ligne place la valeur 1348 en mémoire à l’adresse 2 et
associe l’étiquette lln à cette adresse. Enfin, la troisième ligne
place la valeur 6000 en mémoire à l’adresse suivante (4) et associe
l’étiquette charleroi à cette adresse. La Fig. 6 présente
comment le simulateur affiche ces différentes étiquettes et les valeurs
associées.
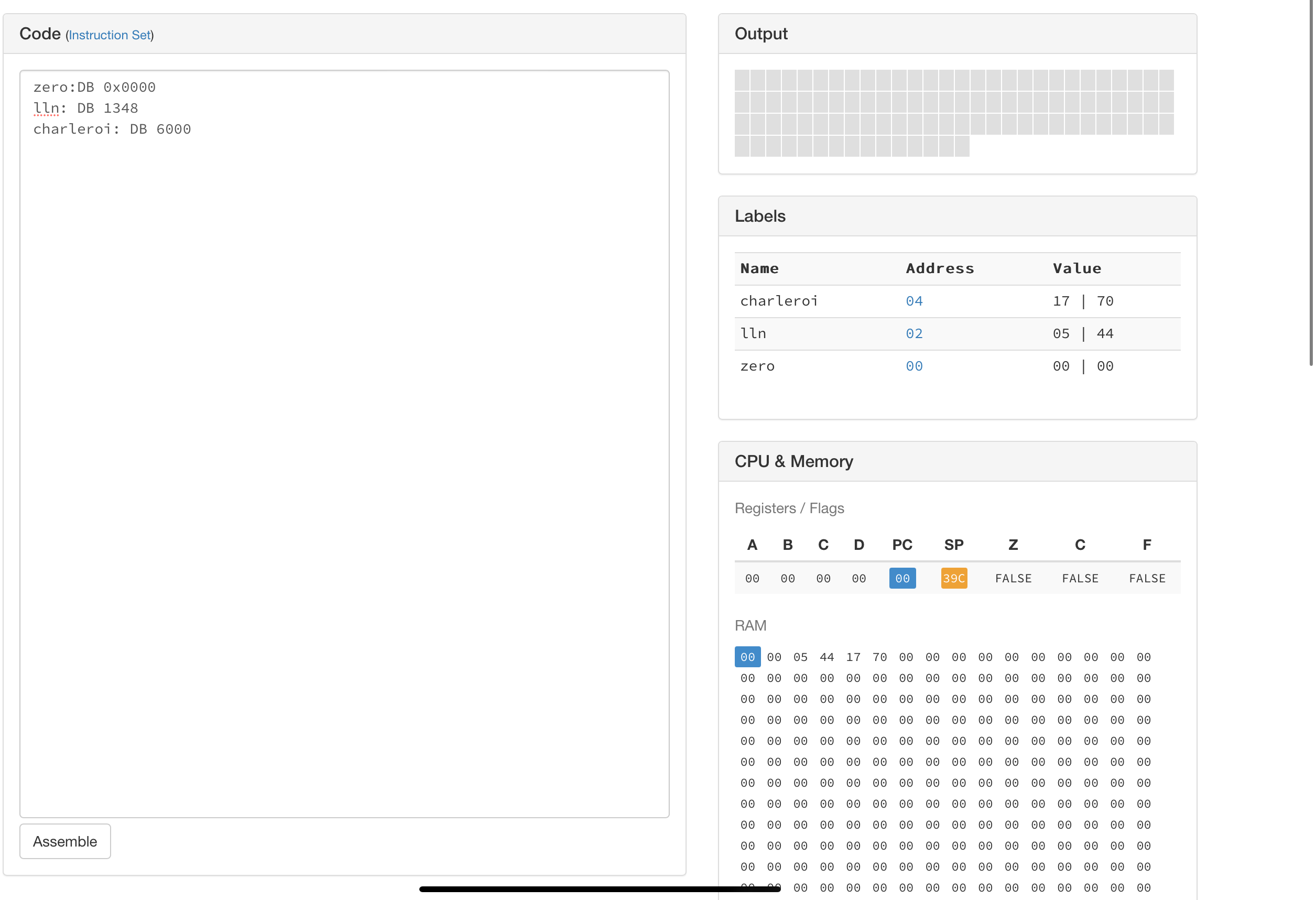
Fig. 6 Exemple d’utilisation du mot-clé DB¶
Les instructions de l’assembleur telles que MOV peuvent
utiliser des étiquettes de deux façons différentes. Tout d’abord,
si une étiquette apparaît dans une instruction en assembleur, elle
est automatiquement remplacée par l’adresse mémoire à laquelle elle
correspond. Si cette étiquette est placée entre crochets ([ et
]), alors le processeur ira chercher la donnée qui se trouve en
mémoire à l’adresse de l’étiquette.
Le programme ci-dessous définit deux étiquettes: x et y. Il
initialise la valeur stockée à l’adresse x à 3 et celle
stockée à l’adresse y à 7 via les deux commandes
DB. La première instruction place dans le registre
A la valeur qui se trouve en mémoire à l’adresse de l’étiquette
x, c’est-à-dire la valeur 3. La deuxième instruction
place dans le registre B la valeur qui se trouve en mémoire
à l’adresse de l’étiquette y, c’est-à-dire la valeur 7.
Ensuite, l’instruction ADD place la valeur 10 dans le registre
A.
MOV A, [x]
MOV B, [y]
ADD A, B
HLT
; Variables et données du programme
x: DB 3
y: DB 7
Lorsque le programme ci-dessus est transformé en langage machine et
stocké en mémoire, l’instruction HLT se trouve à l’adresse
0x12. L’étiquette x correspond à l’adresse 0x14 et y à
l’adresse 0x16 comme illustré dans la Fig. 7.
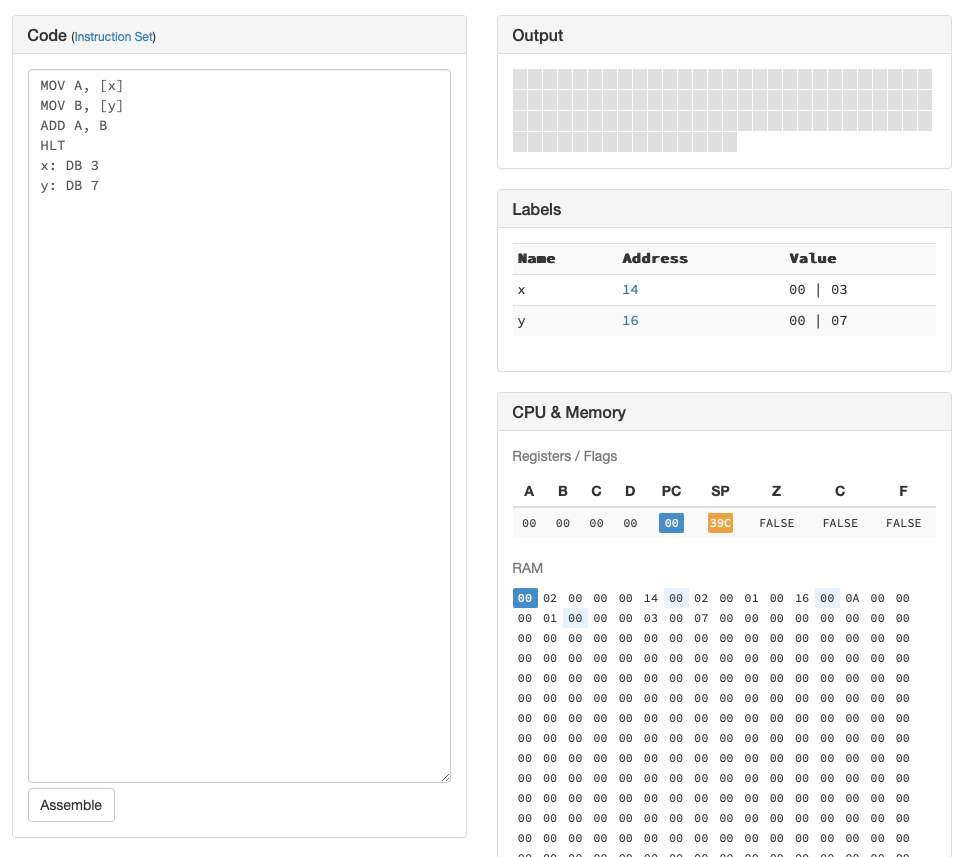
Fig. 7 Adresses mémoires des étiquettes x et y¶
A ce stade, il est utile d’analyser un peu plus en détails la façon dont les
instructions sont encodées en mémoire. Pour le processeur, une instruction en
assembleur est aussi encodée sous la forme d’une séquence de bits. C’est
ce que nous voyons dans la mémoire RAM présentée dans la Fig. 7.
Analysons cette mémoire bloc de 16 bits par bloc de 16 bits. Le premier bloc,
la notation 0x00 02 correspond au code opératoire (ou opcode en anglais)
de l’instruction qui permet de déplacer une information se trouvant en mémoire
vers un registre. Cette instruction prend deux arguments :
un registre
une adresse
Le bloc de 16 bits à l’adresse 0x02 qui a comme valeur 0x00 00 correspond
au registre A. Le bloc de 16 bits à l’adresse 0x04 contient lui la
valeur 0x00 14 qui est l’adresse de l’étiquette x. Ces 6 premiers octets
(0x00 02 00 00 00 14`) sont la représentation binaire de l’instruction
MOV A, [14]. Les six octets qui suivent (0x00 02 00 01 00 16) correspondent
eux à l’instruction MOV B, [16]. Le code opératoire de l’instruction ADD
est 0x00 0A et les 6 octets 0x00 0A 00 00 00 01 représentent bien l’instruction
ADD A, B. L’instruction HLT a comme code opératoire le bloc de 16 bits
0x00 00. Le simulateur définit un code opératoire pour chaque variante d’une
instruction. En voici quelques unes à titre d’illustration :
HLTa comme code opératoire0x00 00
MOVa comme code opératoire0x00 01lorsque ses deux arguments sont des registres
MOVa comme code opératoire0x00 06lorsque son premier argument est un registre et le seconde une constante
ADDa comme code opératoire0x00 0Alorsque ses deux arguments sont des registres
SUBa comme code opératoire0x00 0Dlorsque ses deux arguments sont des registres
INCa comme code opératoire0x00 12et est suivi d’un identifiant de registre
DECa comme code opératoire0x00 13et est suivi d’un identifiant de registre
MULa comme code opératoire0x00 3Cet est suivi identifiant de registre
Connaissant cette représentation des instructions en assembleur sous
la forme de séquence de bits, il est possible (mais pas recommandé) d’écrire
un programme assembleur en utilisant uniquement les commandes DB pour initialiser
la mémoire. Pouvez-vous prévoir ce que fait le « programme » présenté ci-dessous ?
DB 0x0012
DB 0x0001
DB 0x0001
DB 0x0003
DB 0x0001
DB 0
Nous pouvons maintenant lister tous les arguments possibles de l’instruction MOV:
MOV reg1, reg2(reg1etreg2sont des identifiants de registres) : place dansreg1la valeur se trouvant actuellement dansreg2. Le contenu dereg2n’est pas modifié
MOV reg, cst(regest un identifiant de registre etcstune constante) : place dans le registreregla valeurcst
MOV reg, adr(regest un identifiant de registre etadrune adresse en mémoire ou une étiquette) : place dansregl’adresseadr
MOV reg, [adr](regest un identifiant de registre etadrune adresse en mémoire ou une étiquette) : place dansregla valeur se trouvant en mémoire à l’adresseadr
MOV adr, reg(regest un identifiant de registre etadrune adresse en mémoire ou une étiquette) : place la valeur se trouvant dans le registreregen mémoire à l’adresseadr
Les instructions ADD et SUB prennent les mêmes arguments que les quatre
premiers types d’instruction
MOV (le résultat de ADD et SUB se trouve toujours dans un registre).
Les instructions INC et DEC ne prennent qu’un registre comme
argument.
Les instructions MUL et DIV supportent elles trois types d’arguments:
MUL reg(regest un identifiant de registre) : place dans le registreAle résultat du produit entre la valeur se trouvant dans le registrereget le registreA.
MUL cst(cstest une valeur entière) : place dans le registreAle résultat du produit entre la valeur entière passée en argument et le registreA.
MUL [adr](adrest une adresse en mémoire ou une étiquette) : place dans le registreAle résultat du produit entre la valeur se trouvant à l’adresse passée en argument et le registreA.
L’instruction DIV prend également ces trois types d’arguments.
Avec ces instructions qui permettent de manipuler des données se trouvant en mémoire, il est possible de gérer des variables et de réaliser des opérations arithmétiques sur ces variables en mémoire. A titre d’exemple, considérons le programme python ci-dessous.
x=3
y=5
z=x+2*y
Lors de son exécution, ce programme place dans la variable z la
valeur 13. Pour écrire un programme équivalent en assembleur, nous
devons d’abord réserver une zone mémoire pour stocker chacune des
trois variables. Cela se fait en utilisant les trois lignes en
fin de programme avec le mot-clé DB. Nous initialisons la variable
z à la valeur 0. Ces zones mémoire étant définies et initialisées,
nous pouvons d’abord calculer l’expression \(2*y\) et stocker son
résultat dans le registre A. Ensuite, il suffit d’ajouter
le contenu de la variable x au résultat obtenu et de sauver le
résultat de l’addition à l’adresse de la variable z.
MOV A, [y] ; place la valeur de la variable y dans A
MUL 2 ; multiplie le contenu de A par 2
ADD A, [x] ; ajoute au contenu de A la valeur de la variable x
MOV z, A ; sauvegarde du résultat du calcul dans la variable z
HLT
; Variables et données du programme
x: DB 3
y: DB 5
z: DB 0
En mathématiques, on sait que les expressions \(x*x-y*y\) et
\((x-y)*(x+y)\) sont équivalents. Vérifions en python et
en assembleur que c’est bien le cas lorsque la variable x
vaut 9 et la variable y vaut 2.
x=9
y=2
z1=x*x-y*y
z2=(x-y)*(x+y)
Pour traduire ces lignes de python en assembleur, nous
devons découper les expressions mathématiques en sous-expressions
qui sont réalisables avec les instructions ADD, SUB et MUL.
Commençons par l’expression \(x*x-y*y\). Nous pouvons d’abord
calculer les deux carrés et les stocker dans deux registres avant
de réaliser la soustraction.
MOV A, [y] ; place la valeur de la variable y dans A
MUL A ; multiplie le contenu de A par lui-même
MOV B, A ; sauvegarde du résultat dans le registre B
MOV A, [x] ; place la valeur de la variable x dans A
MUL A ; multiplie le contenu de A par lui-même
SUB A, B ; soustraction des deux carrés
MOV z1, A ; sauvegarde du résultat du calcul dans la variable z1
MOV A, [x] ; place la valeur de la variable x dans A
SUB A, [y] ; calcul de x-y
MOV B, [x] ; place la valeur de la variable x dans B
ADD B, [y] ; calcul de x+y
MUL B
MOV z2, A ; sauvegarde du résultat du calcul dans la variable z2
HLT
; Variables et données du programme
x: DB 9
y: DB 2
z1: DB 0
z2: DB 0
En exécutant ce programme dans le simulateur, on peut facilement vérifier
que les zones mémoires étiquetées z1 et z2 contiennent bien le même naturel
avec l’exécution du programme.
Instructions logiques¶
Comme nous l’avons indiqué précédemment, un microprocesseur manipule des séquences de bits. Outre les opérations arithmétiques que nous venons de voir, il est parfois intéressant de réaliser des opérations directement sur les séquence de bits. Cela se fait en utilisant les instructions logiques qui s’appuient sur les opérations booléennes. Une opération booléenne est une fonction qui prend en entrée 0, 1 ou plusieurs bits et retourne un résultat.
Fonctions booléennes¶
La fonction booléenne la plus simple est la fonction identité. Elle prend comme entrée un bit et retourne la valeur de ce bit. On peut la définir en utilisant une table de vérité qui indique la valeur du résultat de la fonction pour chaque valeur possible de son entrée. Dans la table ci-dessous, la colonne x contient les différentes valeurs possibles de l’entrée x et la valeur du résultat pour chacune des valeurs possibles de x.
x |
identité(x) |
0 |
0 |
1 |
1 |
Cette fonction n’est pas très utile en pratique. Elle nous permet d’illustrer une table de vérité simple dans laquelle il y a une valeur binaire en entrée et une valeur binaire également en sortie.
Une fonction plus intéressante est l”inverseur, aussi dénommée NOT(x) en anglais. Cette fonction prend comme entrée un bit. Si le bit d’entrée vaut 1, elle retourne 0. Tandis que si le bit d’entrée vaut 0, elle retourne 1. Cette fonction sera très fréquemment utilisée pour construire des circuits électroniques.
x |
NOT(x) |
0 |
1 |
1 |
0 |
Il y a encore deux fonctions que l’on peut construire avec une seule entrée binaire. La première, baptisée Toujours0, retourne toujours la valeur 0, quelle que soit son entrée. La seconde, baptisée Toujours1 retourne toujours la valeur 1. Voici leurs tables de vérité.
x |
Toujours0(x) |
0 |
0 |
1 |
0 |
x |
Toujours1(x) |
0 |
1 |
1 |
1 |
La logique booléenne devient nettement plus intéressante lorsque l’on considère des fonctions qui prennent plus d’une entrée.
Fonctions booléennes à deux entrées¶
Plusieurs fonctions booléennes classiques existent. Les premières correspondent à la conjonction (et) et à la disjonction (ou) en logique. Commençons par la fonction AND. Celle-ci correspond à la table de vérité suivante:
x |
y |
AND(x,y) |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Cette table comprend quatre lignes qui correspondent à toutes les combinaisons possibles des deux entrées de la fonction. On remarque aisément que la fonction AND(x,y) retourne la valeur 1 uniquement lorsque ses deux entrées ont la valeur 1. Si une des deux entrées de la fonction AND(x,y) a la valeur
0, alors sa sortie est nécessairement 0. Cette fonction est bien l’équivalent de la conjonction logique si l’on applique la convention que 0 représente la valeur Faux.
La fonction OR(x,y), quant à elle, est l’équivalent de la disjonction logique. Sa table de vérité est reprise ci-dessous.
x |
y |
OR(x,y) |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
On remarque aisément que la fonction OR(x,y) correspond bien à la disjonction logique lorsque 1 représente la valeur Vrai. Cette fonction OR(x,y) ne retourne la valeur 0 que si ses deux entrées valent 0. Dans tous les autres cas, elle retourne la valeur 1.
Ces fonctions peuvent être combinées entre elles. Un premier exemple est d’appliquer un inverseur (opération NOT au résultat de la fonction AND). Cette fonction booléenne s’appelle généralement NAND(x,y) (NOT AND) et sa table de vérité est la suivante. On pourra dire que \(NAND(x,y) \iff NOT(AND(x,y))\).
x |
y |
NAND(x,y) |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
De même, la fonction NOR(x,y) s’obtient en inversant le résultat de la fonction OR. On pourra dire que \(NOR(x,y) \iff NOT(OR(x,y))\).
x |
y |
NOR(x,y) |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
Il est important de noter que NOR(x,y) n’est pas équivalent à la fonction OR(NOT(x),NOT(y)). La table de vérité de cette dernière fonction est reprise ci-dessous.
x |
y |
NOT(x) |
NOT(y) |
OR(NOT(x),NOT(y)) |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
Il existe d’autres fonctions booléennes à deux entrées qui sont utiles en pratique. Parmi celles-ci, on retrouve la fonction XOR(x,y) qui retourne la valeur 1 uniquement si une seule de ses entrées a la valeur 1. Sa table de vérité est reprise ci-dessous. On remarquera qu’elle diffère de celle des autres fonctions booléennes que nous avons déjà présenté.
x |
y |
XOR(x,y) |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Ces opérations logiques peuvent être réalisées bit à bit sur des blocs de 16 bits tels que ceux qui sont stockés dans les registres de notre processeur ou en mémoire. On peut aisément définir l’opération NOT sur le mot de 16 bits \(b_{15}b_{14}b_{13}b_{12}b_{11}b_{10}b_{9}b_{8}b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}b_{0}\) comme suit:
\(NOT(b_{15}b_{14}b_{13}b_{12}b_{11}b_{10}b_{9}b_{8}b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}b_{0})=\\not(b_{15})not(b_{14})not(b_{13})not(b_{12})not(b_{11})not(b_{10})not(b_{9})not(b_{8})not(b_{7})not(b_{6})not(b_{5})not(b_{4})not(b_{3})not(b_{2})not(b_{1})not(b_{0})\) où \(not(...)\) est l’opération NOT appliquée à un bit définie plus haut.
De la même façon, on peut définir les opérations qui prennent deux arguments telles que OR ou AND comme suit:
\(OR(a_{15}a_{14}a_{13}a_{12}a_{11}a_{10}a_{9}a_{8}a_{7}a_{6}a_{5}a_{4}a_{3}a_{2}a_{1}a_{0},b_{15}b_{14}b_{13}b_{12}b_{11}b_{10}b_{9}b_{8}b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}b_{0})=\\or(a_{15},b_{15})or(a_{14},b_{14})or(a_{13},b_{13})or(a_{12},b_{12})or(a_{11},b_{11})or(a_{10},b_{10})or(a_{9},b_{9})\\or(a_{8},b_{8})or(a_{7},b_{7})or(a_{6},b_{6})or(a_{5},b_{5})or(a_{4},b_{4})or(a_{3},b_{3})or(a_{2},b_{2})or(a_{1},b_{1})or(a_{0},b_{0})\) où \(or(...)\) est l’opération OR appliquée à un bit définie plus haut.
Ces opérations logiques existent sous trois formes en fonction de leurs arguments:
OR reg1, reg2: place dans le registrereg1le résultat de l’opérationORappliquée aux valeurs stockées dans les registresreg1etreg2
OR reg1, [adr]: place dans le registrereg1le résultat de l’opérationORappliquée aux valeurs stockées dans le registrereg1et en mémoire à l’adresseadr
OR reg1, c: place dans le registrereg1le résultat de l’opérationORappliquée aux valeurs stockées dans le registrereg1et la constantec
Ces instructions permettent d’utiliser ces opérations logiques sur des blocs de 16 bits. En pratique, elles s’avèrent aussi très utile lorsque l’on souhaite fixer des valeurs à certains bits en particulier. Considérons par exemple le bloc de 16 bits \(b_{15}b_{14}b_{13}b_{12}b_{11}b_{10}b_{9}b_{8}b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}b_{0}\) qui est actuellement stocké dans le registre A.
Si l’on souhaite forcer le bit de poids faible à la valeur 0 sans changer aucun des autres bits de ce bloc, il suffit d’exécuter l’instruction AND A, 1111111111111110b. Le lecteur attentif vérifiera aisément que \(AND(b,1)\) vaut \(b\) et que \(AND(b,0)\) vaut toujours \(0\), quelle que soit la valeur du bit \(b\).
L’instruction OR permet elle de forcer la valeur d’un bit à 1. Ainsi OR A, 1000000000000000b forcera la valeur du bit de poids fort du registre A à 1 sans changer les valeurs des autres registres.
Le langage python supporte également les opérations booléennes bit à bit. Les principales sont listées ci-dessous:
En python AND(a,b) s’écrit
a & bEn python OR(a,b) s’écrit
a | bEn python NOT(a) s’écrit
~ aEn python XOR(a,b) s’écrit
a ^ b
Instructions de manipulation de bits¶
Notre processeur supporte également des opérations de décalage à gauche (SHL - SHift Left) et à droite (SHR - SHift Right). Ces instructions prennent deux arguments comme les opérations arithmétiques. En pratique, ces instructions sont généralement utilisées avec une constante comme second argument.
L’instruction SHL reg, n décale de n positions les bits se trouvant dans le registre reg vers la gauche. A titre d’exemple, si le registre B contient les bits \(b_{15}b_{14}b_{13}b_{12}b_{11}b_{10}b_{9}b_{8}b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}b_{0}\), alors après exécution de l’instruction SHL B, 3 ce registre contiendra les bits \(b_{12}b_{11}b_{10}b_{9}b_{8}b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}b_{0}000\). De façon équivalente, si on exécute SHR B, 5 sur les bits \(b_{15}b_{14}b_{13}b_{12}b_{11}b_{10}b_{9}b_{8}b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}b_{0}\), on obtient \(00000b_{15}b_{14}b_{13}b_{12}b_{11}b_{10}b_{9}b_{8}b_{7}b_{6}b_{5}\).
Il est aussi possible de demander à python d’effectuer des décalages à gauche et à droite. Ainsi, x << p décale la représentation binaire de x de p positions vers la gauche. De la même façon, y >> p décale la représentation binaire de y de p positions vers la droite.
L’instruction de comparaison¶
Outre les instructions arithmétiques et logiques, notre processeur contient également une instruction de comparaison dénommée CMP. Cette instruction permet de comparer deux séquences de bits pour déterminer si elles sont égales. Elle compare la valeur se trouvant dans le registre qui est son premier argument avec son second argument qui peut être :
un autre registre (
CMP reg1, reg2)une valeur se trouvant à une adresse en mémoire (
CMP reg, [adr])une constante (
CMP reg, cst)
Lors de son exécution, l’instruction de comparaison ne modifie pas
la valeur contenue dans le registre qui est son premier argument. Elle stocke
son résultat dans un drapeau (flag en anglais). Ce drapeau occupe 1 bit dans le
processeur (le bit Z). Il est mis à la valeur vrai par l’instruction CMP si
les valeurs des deux arguments sont identiques et à faux sinon. Dans l’exemple ci-dessous,
le drapeau Z est mis à la valeur faux après exécution de la première instruction
CMP. Ce drapeau passe à la valeur vrai après exécution de la seconde
instruction CMP.
MOV A, 2
MOV B, 3
MOV C, 2
CMP A, B ; Z est mis à faux
CMP A, C ; Z est mis à vrai
L’instruction CMP n’est pas la seule à modifier le drapeau Z. C’est le cas
pour toutes les instructions arithmétiques et logiques: ADD, SUB, MUL,
INC, DEC, … Après exécution de chacune de ces instructions, le drapeau
Z est mis à vrai si le résultat de l’opération est le bloc de 16 bits
dont tous les bits valent zéro. Lorsque l’on veut utiliser la valeur du drapeau
Z, il faut le faire immédiatement après l’exécution de l’instruction CMP.
Notre processeur supporte un deuxième drapeau, Carry (report en anglais)
ou C. Ce drapeau est utilisé par les opérations arithmétiques et logiques.
Notre processeur stocke des données sur 16 bits dans chacun de ses registres.
Lorsque l’on réalise une opération arithmétique, il est possible que le résultat
nécessite plus de 16 bits pour stocker sa représentation binaire. C’est
le cas par exemple pour les opérations d’addition ou de multiplication. Dans le programme
ci-dessous, le drapeau C sera mis à vrai à la seconde instruction INC car
le résultat (65536`) doit être stocké sur 17 bits et non 16.
MOV A, 65534
INC A ; C mis à faux
INC A ; C mis à vrai
Il en va de même pour l’instruction de multiplication qui provoque également
un dépassement de capacité (et donc fixe le drapeau C à vrai après
son exécution) comme dans l’exemple ci-dessous.
MOV A, 40000
MUL A ; dépassement de capacité C est mis à vrai
Le compteur de programme et les instructions de saut¶
Outre les registres A, B, C et D, un microprocesseur contient
également un registre spécial généralement dénommé Compteur de Programme
ou Program Counter (PC) en anglais. Certains documents
parlent de pointeur d’instruction ou instruction pointer en
anglais. Dans ce syllabus, nous
utiliserons le terme PC pour parler de ce registre. Le PC stocke
à tout moment l’adresse en mémoire de l’instruction à exécuter. Lors de l’exécution
d’une instruction arithmétique, le PC est simplement incrémenté de
façon à contenir l’adresse de l’instruction suivante. A titre d’exemple, considérons
la suite d’instructions de la section précédente.
i1: MOV A, 2
i2: MOV B, 3
i3: MOV C, 2
i4: CMP A, B
i5: CMP A, C
Au démarrage de l’ordinateur, le PC est initialisé à l’adresse
de la première instruction à exécuter (0 dans notre processeur simple, mais
ce n’est pas toujours le cas). Durant l’exécution de l’instruction
MOV A,2, le PC contient l’adresse de l’étiquette i1. A
la fin de l’exécution de cette instruction, le PC est modifié pour
contenir l’adresse de l’instruction qui suit, c’est-à-dire i2. Cette
mise à jour du compteur de programme s’effectue lors de l’exécution de toutes les
instructions arithmétiques et logiques. Cela permet l’exécution séquentielle
des instructions du programme.
Notre microprocesseur, comme tous les autres processeurs, supporte également des instructions qui permettent de modifier la valeur stockée dans le PC. Ce sont les instructions de saut. Il existe deux types d’instructions de saut:
les instructions de saut inconditionnelles qui permettent de remplacer l’adresse stockée dans le PC par une autre adresse.
les instructions de saut conditionnelles qui permettent de remplacer l’adresse stockée dans le PC par une autre adresse lorsqu’une condition particulière est remplie. Si la condition n’est pas remplie, l’adresse stockée dans le PC devient celle de l’instruction suivante.
L’instruction de saut inconditionnelle s’appelle JMP (pour jump, saut
en anglais). Cette instruction prend un argument qui est une adresse (ou une étiquette).
A titre d’illustration, considérons la suite d’instructions ci-dessous. A votre avis,
l’instruction CMP va-t-elle mettre le drapeau Z à vrai ou faux ?
i1: MOV A, 2
i2: JMP i4
i3: MOV A, 9
i4: MOV B, 9
i5: CMP A, B
La première instruction place la valeur 2 dans le registre A. La deuxième
instruction (étiquette i2) modifie le compteur de programme de façon à ce
que l’adresse de l’instruction suivante soit celle de l’étiquette i4. Le
processeur exécute donc ensuite l’instruction MOV B,9 qui se trouve à l’adresse
de l’étiquette i4. Ensuite il exécute l’instruction de comparaison qui place
la valeur faux dans le drapeau Z puisque le registre A contient la valeur
2 et le registre B la valeur 9.
L’instruction de saut inconditionnel a plusieurs utilisations comme nous le
verrons bientôt. Pour rendre le code assembleur plus facile à lire, il
est intéressant de définir les constantes au début du programme plutôt qu’à la
fin. Comme le processeur commence par exécuter l’instruction se trouvant à l’adresse
0, nous ne pouvons pas commencer un programme par le mot clé DB pour définir une
constante. Par contre, nous pouvons facilement associer une étiquette start
au début « réel » de notre programme et avoir comme première instruction JMP start.
Cette instruction peut être suivie d’une définition des différentes constantes utilisées
par le programme avec une suite de mot-clés DB et les étiquettes associées.
A titre d’exemple, reprenons le programme python ci-dessous.
x=3
y=5
z=x+2*y
Ce programme peut être de façon plus lisible comme suit.
JMP start
; Variables et données du programme
x: DB 3
y: DB 5
z: DB 0
start: MOV A, [y] ; place la valeur de la variable y dans A
MUL 2 ; multiplie le contenu de A par 2
ADD A, [x] ; ajoute au contenu de A la valeur de la variable x
MOV z, A ; sauvegarde du résultat du calcul dans la variable z
HLT
Nous pouvons maintenant aborder les instructions de saut conditionnelles. Ces
instructions réalisent la modification du PC en fonction des valeurs
des drapeaux Z et/ou C. Ces instructions prennent un seul argument: l’adresse
qu’il faut placer dans le PC si la condition est remplie.
Les deux premières instructions conditionnelles sont JE (Jump if Equal)
et JNE (Jump if Not Equal). Ces instructions s’utilisent après
une instruction CMP et testent la valeur du drapeau Z. L’instruction
JE modifie le PC si le drapeau Z contient la valeur
vrai. L’instruction JNE, elle, modifie le PC
lorsque le drapeau Z contient la valeur faux.
Imaginons que nous devions écrire un programme qui place la valeur 0 dans
le registre C si les valeurs contenues dans les registres A et B sont
égales et 1 sinon. Une première version de ce programme pourrait
s’écrire comme suit.
MOV A, 123
MOV B, 123
CMP A, B
JE equal
MOV C, 0
equal: MOV C, 1
HLT
Lors de son exécution, ce programme charge les deux valeurs dans les registres
A et B. Ensuite, l’instruction CMP fixe la valeur du drapeau Z. Si ce
drapeau est à la valeur vrai, l’instruction JE modifie
le PC pour y mettre l’adresse correspondant à l’étiquette equal et
l’instruction MOV C,1 est exécutée. Par contre, si le drapeau est
à la valeur faux, le processeur exécute l’instruction MOV C,0 et place
la valeur attendue dans le registre C. Malheureusement, l’instruction
suivante est MOV C, 1 et la valeur de ce registre est à nouveau modifiée.
On peut éviter ce problème en utilisant un saut inconditionnel après l’exécution
de l’instruction MOV C,0 comme ci-dessous.
MOV A, 123
MOV B, 123
CMP A, B
JE equal
ne: MOV C, 0
JMP suite:
equal: MOV C, 1
suite: HLT
Dans cette séquence d’instructions, le saut inconditionnel permet d’empêcher
l’exécution de l’instruction se trouvant à l’adresse correspondant à l’étiquette
equal. C’est une utilisation assez fréquente de l’instruction de saut
inconditionnel comme nous le verrons bientôt.
Il existe une deuxième paire d’instructions de saut qui testent uniquement
la valeur du drapeau Z: JZ (Jump if Zero) et JNZ
(Jump if Not Zero). L’instruction
JZ modifie le PC si le drapeau Z est à la valeur vrai.
L’instruction JNZ réalise cette modification lorsque le drapeau
Z contient la valeur faux. Ces instructions peuvent s’utiliser sans être
précédées de l’instruction CMP comme dans l’exemple ci-dessous.
MOV A, 1
DEC A
JZ zero
nz: MOV C, 1
JMP suite:
zero: MOV C, 0
suite: HLT
Les instructions conditionnelles permettent aussi de réaliser des comparaisons pour
déterminer si la valeur stockée dans un registre est supérieure, inférieure, ou inférieure
ou égale à celle d’un autre registre. Ces instructions s’utilisent directement après
une opération CMP reg1, reg2. Les instructions suivantes sont supportées
par notre assembleur:
JA (Jump Above): le saut conditionnel est effectué si la valeur stockée dans le premier registre argument de l’instruction
CMPest strictement supérieure à la valeur stockée dans le second registreJB (Jump Below): le saut conditionnel est effectué si la valeur stockée dans le premier registre argument de l’instruction
CMPest strictement inférieure à la valeur stockée dans le second registreJAE (Jump Above or Equal): le saut conditionnel est effectué si la valeur stockée dans le premier registre argument de l’instruction
CMPest supérieure ou égale à la valeur stockée dans le second registreJBE (Jump Below or Equal): le saut conditionnel est effectué si la valeur stockée dans le premier registre argument de l’instruction
CMPest inférieure ou égale à la valeur stockée dans le second registre
A titre d’exemple, nous pouvons utiliser ces instructions conditionnelles pour
implémenter un petit programme qui calcule la valeur absolue de la différence
entre deux variables et place le résultat dans le registre C.
JMP start
; déclarations des variables et constantes
x: DB 12
y: DB 9
start: MOV A, [x]
CMP A, [y]
JBE petit
MOV C, A
SUB C, [y]
JMP fin
petit: MOV C, [y]
SUB C, A
fin: HLT
Enfin, il est aussi possible de vérifier simplement le drapeau C via les
instructions JC (Jump if Carry) et JNC (Jump if Not Carry).
Ces instructions sont utiles pour détecter un dépassement de capacité, notamment
sur les opérations arithmétiques telles que la multiplication. En cas de dépassement,
il est parfois préférable d’avertir l’utilisateur ou d’arrêter l’ordinateur
plutôt que que continuer l’exécution du programme avec des données erronées dans
un registre qui pourraient provoquer des erreurs en cascade. L’exemple ci-dessous
montre comme utiliser l’instruction JNC pour vérifier si une instruction
de multiplication a provoqué un dépassement de capacité.
MOV A, 1000
MOV B, 123
MUL B
JNC correct
; dépassement de capacité
HLT
correct: MOV B, D
; suite du programme
Un autre problème mathématique qui peut survenir est lorsque l’on effectue
une division par zéro. Contrairement à d’autres microprocesseurs,
notre microprocesseur ne dispose pas de drapeau qui permet
de détecter cette situation. Lors de l’exécution d’une instruction telle que DIV 0,
le processeur s’arrête et affiche le message Division by 0. Si vous souhaitez
éviter qu’un programme qui réalise une division ne s’arrête de cette façon, vous devez
vous assurer de ne jamais avoir 0 comme diviseur dans un de vos quotients.
Les instructions conditionnelles¶
Les instructions de saut que nous venons de voir jouent un rôle critique dans les
programmes écrits en assembleur. C’est grâce à ces instructions que l’on peut
implémenter à la fois des instructions conditionnelles de type if ... else, mais
aussi les boucles et même les appels à des fonctions et procédures comme nous le
verrons plus tard.
En python, il est facile d’écrire une instruction conditionnelle. Il suffit
d’utiliser le mot clé if, d’indiquer la condition et ensuite la
séquence d’instructions à exécuter. Prenons comme exemple la recherche du
maximum entre deux variables, x et y. En python, on peut affecter le
maximum à la variable max comme suit:
if x>y :
max=x
else:
max=y
En assembleur, nous devons utiliser une instruction de saut conditionnelle pour
obtenir le même résultat. Commençons pas déclarer nos trois variables: x,
y et max. Ensuite nous devons comparer les valeurs des variables
x et y. Pour cela, nous les plaçons dans les registres A et B.
Si la valeur de la variable x est strictement supérieure
à celle de la variable y, nous devons placer la valeur de x (qui est
actuellement dans le registre A) dans la variable max. Sinon, nous plaçons
la valeur de la variable y dans la zone mémoire correspondant à la
variable max.
JMP start
; déclarations et initialisations des variables
x: DB 12
y: DB 9
max: DB 0
start: MOV A, [x]
MOV B, [y]
CMP A, B
JA xmax
MOV max, B
JMP fin
xmax: MOV max, A
fin: HLT
Une approche similaire peut être utilisée pour implémenter d’autres instructions conditionnelles. Le tout est de ramener toute condition à une comparaison avec la valeur 0 ou à une relation d’ordre.
Pour les conditions plus complexes, il faut parfois réécrire l’instruction conditionnelle. Prenons deux exemples en python pour illustrer cette réécriture.
if (a>0) AND (b<1):
x=2
Dans ce cas, on peut réécrire l’instruction conditionnelle sous la forme :
if (a>0) :
if (b<1) :
x=2
Ces deux instructions conditionnelles imbriquées peuvent facilement s’implémenter avec les instructions de saut conditionnel que nous avons présentées. Il en va de même pour une disjonction logique. L’instruction ci-dessous :
if (a>0) OR (b<1):
x=3
peut se réécrire de la façon suivante pour supprimer la disjonction logique.
if (a>0) :
x=3
else :
if (b<1) :
x=2
Les lecteurs attentifs convertiront ces instructions conditionnelles en assembleur à titre d’exercice.
Les boucles¶
Après les opérations arithmétiques et logiques et les instructions conditionnelles, il nous reste à voir comment supporter les boucles. Python supporte deux types principaux de boucles :
les boucles
whileles boucles
for
Les boucles while sont les boucles les plus générales. Une boucle for est
équivalente à une boucle d’un type particulier qui est écrite de façon compacte.
Nous nous focaliserons sur les boucles while dans cette section. Une boucle
while comprend toujours une condition qui comprend une expression booléenne
qui est testée à chaque itération et un corps contenant une ou plusieurs instructions
à exécuter.
Commençons par une boucle inutile, mais que vous avez probablement déjà rencontrée: la boucle infinie.
while True:
x=x+1
En assembleur, cette boucle peut s’écrire en utilisant une instruction
de saut inconditionnel JMP.
JMP start
; variables et constantes
x: DB 0
; programme
start: MOV A, [x]
INC A
MOV x, A
JMP start
Parfois, on écrit par inadvertance une boucle infinie en python car la condition d’arrêt de la boucle n’est jamais réalisée, même si python vérifie cette condition à chaque itération.
x=1
while x!=0:
x=x+1
Ce programme python peut être traduit par les instructions suivantes en assembleur.
JMP start
; variables et constantes
x: DB 1
start: MOV A, [x]
CMP A, 0
JZ fin
INC A
MOV x, A
JMP start
fin: HLT
Ce programme place la valeur de la variable x dans le registre A et
regarde si elle est différente de zéro. Si cette valeur est égale à zéro, il
sort de la boucle. Sinon, il incrémente la valeur du registre A puis sauve
le résultat en mémoire à l’adresse de la variable x.
La sauvegarde en mémoire de la valeur de la variable x n’est pas nécessaire
puisque cette valeur se trouve également dans le registre A. On peut réduire
le nombre d’instructions à exécuter et donc accélérer le programme en mettant à jour
la valeur de la variable x uniquement en fin de boucle comme présenté ci-dessous.
JMP start
; variables et constantes
x: DB 1
start: MOV A, [x]
boucle: CMP A, 0
JZ fin
INC A
JMP boucle
fin: MOV x, A
HLT
Cette nouvelle version du programme incrémente la valeur du registre A à chaque
itération mais ne sauvegarde la valeur du registre A en mémoire à l’adresse
de la variable x qu’à la sortie de la boucle (étiquette fin). Ce programme est
plus efficace que le précédent même si il aboutit au même résultat final.
Si vous exécutez le programme python, vous verrez qu’il ne s’arrête jamais et
que vous devrez manuellement arrêter l’interpréteur python pour forcer la
terminaison du programme. Si vous faites le même essai
avec le programme en assembleur sur le simulateur, vous verrez que le programme en
assembleur finit par s’arrêter. Cette différence de comportement s’explique par
la façon dont les nombres naturels sont stockés en python et dans notre assembleur.
Le langage python a été conçu de façon à pouvoir réaliser des calculs sans limitation
avec tous les nombres entiers. Pour cela, le langage python adapte dynamiquement
le nombre de bits utilisés pour représenter chaque nombre. En python,
vous pouvez calculer avec les valeurs 1000, 2000000, `5000000000 ou
9000000000000 sans aucun souci.
Notre assembleur utilise 16 bits pour représenter les nombres naturels. Avec 16 bits
qui peuvent prendre les valeurs 0 et 1, il est possible de représenter
\(2^{16}\) nombres
naturels différents. Le plus petit est 0 (ou 0b00000000 00000000) et le
plus grand 65535 (\(2^{16}-1\) ou 0b11111111 11111111). Analysons ce qu’il
se passe dans la boucle. Au début, la valeur dans le registre A passe de
0b00000000 00000000 à puis 0b000000000 0000001, 0b00000000 00000010, …
Après quelque temps, le registre A contient la valeur 65534 ou 0b11111111 11111110.
Après incrémentation, cette valeur passe à 0b11111111 11111111. C’est le plus
grand naturel que l’on peut représenter en utilisant 16 bits. L’incrémentation
suivante devrait faire passer la valeur du registre à 0b1 00000000 00000000
ou 65536. Comme le registre A ne peut stocker que 16 bits, il conserve
les 16 bits de poids faible, à savoir 0b00000000 0000000 ou 0 en notation
décimale. Après l’exécution de cette instruction, le drapeau C du processeur
est mis à vrai pour indiquer qu’il y a eu un dépassement de capacité lors de l’exécution
de l’instruction INC, mais notre programme ne vérifie pas ce drapeau…
Le nouvelle valeur stockée dans le registre A est numériquement égale à 0
et notre programme sauvegarde la valeur 0 en mémoire puis s’arrête.
Nous pouvons nous inspirer de cette approche pour traduire une boucle while en une
séquence d’instructions en assembleur. Pour cela, notre programme doit :
Évaluer la valeur de la condition
Si la condition est évaluée à la valeur vrai, exécuter le corps de la boucle puis revenir au point 1
Sinon, passer à l’exécution des instructions placées juste après le corps de la boucle
Pour illustrer cette traduction, considérons la boucle ci-dessous. Après l’exécution de
cette boucle, la variable x contient la valeur 512.
x=1
n=1
while (n<10) :
n=n+1
x=x+x
Ce fragment de code peut se traduire en langage assembleur. Il faut d’abord charger
la valeur de la variable n (ligne 5) et la comparer à 10. Si la valeur
de la variable n est
supérieure ou égale à 10, il faut sortir de la boucle. En général, pour implémenter
une condition en assembleur, utilise l’instruction de saut qui correspond à la condition
inverse puisque l’on cherche à faire un saut pour sortir de la boucle si la condition
n’est pas vérifiée. Ensuite, il suffit d’incrémenter la valeur de la variable n
puis de la sauvegarder en mémoire. On peut ensuite charger la variable x dans un
registre et calculer x+x. Enfin, on utilise une instruction de saut inconditionnel
JMP pour revenir au début de la boucle et réévaluer la condition n<10.
JMP boucle
; variables
x: DB 1
n: DB 1
boucle: MOV A, [n]
CMP A, 10
JAE fin
INC A
MOV n, A
MOV B, [x]
ADD B, B
MOV x, B
JMP boucle
fin: HLT
Tout comme dans l’exemple précédent, on aurait pu réduire le nombre de transferts
vers la mémoire et d’instructions en plaçant les variables x et n dans les
registres B et A au début de la boucle, avant l’évaluation de la condition
d’arrêt. Si on procède de cette façon, il ne faut bien entendu pas oublier de
sauver les valeurs stockées dans les registres en mémoire en sortie de boucle.
JMP boucle
; variables
x: DB 1
n: DB 1
MOV A, [n]
MOV B, [x]
boucle: CMP A, 10
JAE finb
INC A
ADD B, B
JMP boucle
finb: MOV n, A ; sauvegarde variable n
MOV x, B ; sauvegarde variable x
fin: HLT
En python, il existe différentes formes de boucles for. Nous nous limiterons
aux boucles qui itèrent sur des naturels comme for i in range (0,4): ou
for x in range (1, 5, 2):. Ces boucles peuvent facilement se traduire sous la
forme d’une boucle while en python. Ainsi, les deux boucles ci-dessous
sont équivalentes.
for x in range(2,7):
print(x)
x=2
while (x<7):
print(x)
x=x+1
De la même façon, les deux boucles ci-dessous sont également équivalentes.
for x in range (10, 5, -2):
print(x)
x=10
while (x>5):
print(x)
x=x-2
Chacune de ces boucles while peut être facilement convertie en assembleur en utilisant notamment des instructions de saut.
Utilisation des tableaux¶
Jusque maintenant, nous avons manipulé des variables entières qui sont stockées en mémoire ou dans des registres. Un ordinateur doit également pouvoir traiter des objets mathématiques tels que les vecteurs et les matrices. Ceux-ci doivent aussi pouvoir être stockés en mémoire.
Commençons par analyser la façon dont un programme peut manipuler les coordonnées (x,y) d’un point sur un plan. Ces coordonnées sont toutes les deux représentées sous la forme d’un naturel. Une première approche serait d’associer une variable pour l’abscisse et une autre pour l’ordonnée. C’est ce que nous faisons dans l’exemple ci-dessous avec les variables CAx
et CAy pour les coordonnées du point A. Le programme doit vérifier si les coordonnées
de deux points sont égales. Pour cela, il charge simplement les
coordonnées x puis y des deux points à comparer et met la variable eq à 1
si les deux points sont égaux et 0 sinon.
JMP start
; mis à 1 si égales, 0 sinon
eq: DB 0
; premier point
CAx: DB 1 ; coordonnée x
CAy: DB 2 ; coordonnée y
; second point
CBx: DB 1 ; coordonnée x
CBy: DB 7 ; coordonnée y
start: MOV A, [CAx]
MOV B, [CBx]
CMP A, B
JNE diff
MOV A, [CAy]
MOV B, [CBy]
CMP A, B
JNE diff
egal:
MOV eq, 1
JMP fin
diff:
MOV eq, 0
fin: HLT
Malheureusement cette solution nous force à définir un très grand nombre de variables. Si on
analyse comment l’assembleur place les données en mémoire, on se rend compte que
les variables CAx et CAy occupent des positions consécutives en mémoire. Il en va
de même pour les variables CBx et CBy. Ainsi, la mémoire initialisée par le programme
ci-dessus peut se visualiser comme dans la table Tableau 7 où l’adresse 03
est utilisée par la variable eq.
adresse |
valeur |
03 |
0 |
05 |
1 |
07 |
2 |
09 |
1 |
0B |
7 |
On peut profiter de cette organisation de la mémoire et déclarer nos variables en utilisant une étiquette pour chaque paire de deux entiers qui représente une coordonnée.
; mis à 1 si égales, 0 sinon
eq: DB 0
; premier point
CA: DB 1 ; coordonnée x
DB 2 ; coordonnée y
; second point
CB: DB 1 ; coordonnée x
DB 7 ; coordonnée y
Ces déclarations définissent deux variables: CA et CB qui utilisent chacune
deux blocs consécutifs de 16 bits en mémoire. Avec ces étiquettes, nous pouvons adapter notre
programme de façon à ce qu’il puisse tester l’égalité des coordonnées x et
y de chaque point. Pour les coordonnées x, c’est facile. Il suffit de réutiliser
les mêmes instructions que dans le programme précédent en adaptant le nom des
variables.
start: MOV A, [CA]
MOV B, [CB]
CMP A, B
JNE diff
Pour comparer les coordonnées y, cette approche ne fonctionne plus car nous n’avons
pas défini d’étiquette correspondant à l’adresse de la coordonnée y du point CA
en mémoire. Par contre, nous savons que cette coordonnée se trouve à l’adresse
qui suit celle de la coordonnée x. Si la coordonnée x se trouve à l’adresse
Adr en mémoire, alors la coordonnée y se trouve à l’adresse Adr+2 puisque
sur notre processeur un entier occupe 16 bits. On voudrait pouvoir écrire les instructions
suivantes :
MOV A, [CA+2]
MOV B, [CB+2]
CMP A, B
JNE diff
Dans ce programme, CA correspond à une adresse en mémoire et CA+2 serait
l’adresse de l’entier 16 bits qui suit celui qui se trouve à l’adresse CA en mémoire.
Malheureusement, notre processeur ne nous permet pas de calculer une adresse
de cette façon dans l’instruction MOV. Il permet de réaliser ce genre de calcul
simple (addition ou soustraction) avec une adresse, mais uniquement si celle-ci se
trouve dans un registre. On doit donc d’abord placer l’adresse CA dans un registre
(par exemple le registre `C avec l’instruction MOV C, CA).
Une fois cette opération réalisée, on peut utiliser
l’adresse se trouvant dans le registre C. Ainsi, l’instruction MOV A, [C] placera
dans le registre A le bloc de 16 bits qui se trouve en mémoire à l’adresse qui se
trouve actuellement dans le registre C. L’instruction MOV B, [C+2] placera
dans le registre B le bloc de 16 bits qui se trouve actuellement en mémoire à l’adresse
qui suit l’adresse qui est dans le registre C. Enfin, l’instruction
MOV D, [C-2] placera dans le registre D le bloc de 16 bits qui se trouve en mémoire
à l’adresse qui précède celle qui est dans le registre C.
Nous pouvons donc écrire les instructions suivantes pour comparer les coordonnées
y
MOV C, [CA]
MOV A, [C+2]
MOV D, [CB]
MOV B, [D+2]
CMP A, B
JNE diff
Note
Notez bien la différence entre les instructions
MOV A, Adr
MOV A, [Adr]
La première place dans le registre A l’adresse qui est son second argument. La seconde place dans le registre A la valeur qui est actuellement stockée en mémoire à l’adresse Adr.
Nous pouvons maintenant écrire le programme complet pour comparer les
coordonnées x et y de nos deux points.
JMP start
; mis à 1 si égales, 0 sinon
eq: DB 0
; coordonnées premier point
CA: DB 1
DB 2
; coordonnées second point
CB: DB 1
DB 2
start:
MOV A, CA
MOV B, CB
MOV C, [A]
MOV D, [B]
CMP C, D
JNE diff
MOV C, [A+2]
MOV D, [B+2]
CMP C, D
JNE diff
egal:
MOV eq, 1
JMP fin
diff:
MOV eq, 0
fin:
HLT
Cette solution peut être étendue pour stocker des vecteurs ou des tableaux d’entiers dont la taille est connue. Pour stocker des coordonnées (x,y,z), il nous suffit de réserver trois mots contigus en mémoire. De la même façon, si l’on doit stocker le nombre de jours dans chaque mois de l’année civile, il suffit de réserver un bloc de 12 mots consécutifs en mémoire et d’y stocker les valeurs reprises dans la Tableau 8.
adresse |
valeur |
m+0 |
31 |
m+2 |
28 |
m+4 |
31 |
m+6 |
30 |
m+8 |
31 |
m+10 |
30 |
m+12 |
31 |
m+14 |
31 |
m+16 |
30 |
m+18 |
31 |
m+20 |
30 |
m+22 |
31 |
Grâce à ce tableau, on peut facilement calculer le nombre de jours dans une année civile. En python, ce programme aurait pu être écrit de la façon suivante.
tableau=[31,28,31,30,31,30,31,31,30,31,30,31]
somme=0
i=0
while(i<12):
somme = somme + tableau[i]
i=i+1
En assembleur c’est un tout petit peu plus compliqué, mais il suffit de bien faire
attention aux instructions que l’on écrit et d’être systématique. Notre programme assembleur
va parcourir le tableau du nombre de jours dans chaque mois. Pour cela, nous aurons besoin
de conserver l’indice du tableau mois qui est en cours de traitement. Nous
choisissons d’utiliser le registre C pour stocker cette information. Il est
initialisé à 0 avant d’entrer dans la boucle. Connaissant cet indice, il est possible
de calculer l’adresse du Cème élément du tableau `mois. Pour cela, il suffit de
calculer la somme entre l’adresse du tableau et le double de l’indice C puisque chaque
entier prend 16 bits et donc deux adresses en mémoire. Nous choisissons d’utiliser le registre
A pour stocker cette adresse car c’est le seul registre qui supporte l’opération de
multiplication. Nous aurions pu aussi prendre le registre D et remplacer l’instruction
MUL 2 par ADD D, D qui donne le même résultat et en pratique est généralement
plus rapide.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | JMP start ; variables jours: DB 0 mois: DB 31 DB 28 DB 31 DB 30 DB 31 DB 30 DB 31 DB 31 DB 30 DB 31 DB 30 DB 31 start: MOV C, 0 ; index dans le tableau boucle: MOV A, C MUL 2 ADD A, mois ; adresse en mémoire du Ceme mois MOV B, [A] ADD B, [jours] MOV jours, B INC C CMP C,11 JA fin JMP boucle fin: HLT |
De façon générale, si un tableau de naturels démarre à l’adresse A, alors le ième élément de ce tableau se trouve en mémoire à l’adresse \(A+2*i\). Cette organisation peut également être utilisée pour stocker des matrices en mémoire. Il suffit simplement de définir une relation entre les indices d’un élément de la matrice et la zone mémoire correspondante. Les deux principales méthodes pour stocker une matrice en mémoire sont ligne par ligne et colonne par colonne.
Pour illustrer ces deux conventions, considérons la matrice à deux lignes et trois colonnes de la Fig. 8.
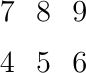
Fig. 8 Une matrice entière composée de deux lignes et trois colonnes
La façon la plus classique pour stocker une telle matrice est de le faire ligne par ligne comme représenté dans la Fig. 9. Dans cette représentation, si la matrice a l lignes et c colonnes, alors l’élément i,j de la matrice se trouve à l’adresse \(A+ 2 \times (i \times c + j)\) en supposant que les indices des lignes et des colonnes commencent à 0.
![\node (l11) at (0,0) {$7$};
\node (l12) at (0.75,0) {$8$};
\node (l13) at (1.5,0) {$9$};
\node (l21) at (0,-0.7) {$4$};
\node (l22) at (0.75,-0.7) {$5$};
\node (l23) at (1.5,-0.7) {$6$};
\node (mem) at (3,0) {Mémoire};
\node (m0) at (3,-1) {\texttt{x} $7$};
\node (m1) at (3,-1.33) {\texttt{x+2} $8$};
\node (m2) at (3,-1.66) {\texttt{x+4} $9$};
\node (m3) at (3,-2) {\texttt{x+6} $4$};
\node (m4) at (3,-2.33) {\texttt{x+8} $5$};
\node (m5) at (3,-2.66) {\texttt{x+10} $6$};
\draw [->,color=blue] (l11.west) |- (m0.west);
\draw [->,color=blue] (l12.west) |- (m1.west);
\draw [->,color=blue] (l13.west) |- (m2.west);
\draw [->,color=green] (l21.east) |- (m3.west);
\draw [->,color=green] (l22.east) |- (m4.west);
\draw [->,color=green] (l23.east) |- (m5.west);](../_images/tikz-8987d040ff76b3c209f7276cb42e511ecba0807d.png)
Fig. 9 Stockage ligne par ligne d’une matrice
Il est aussi possible de stocker cette matrice colonne par colonne comme représenté dans la Fig. 10. Dans cette représentation, si la matrice a l lignes et c colonnes, alors l’élément i,j de la matrice se trouve à l’adresse \(A+ 2 \times (j \times l + i)\) en supposant que les indices des lignes et des colonnes commencent à 0.
![\node (l11) at (0,0) {$7$};
\node (l12) at (0.75,0) {$8$};
\node (l13) at (1.5,0) {$9$};
\node (l21) at (0,-0.7) {$4$};
\node (l22) at (0.75,-0.7) {$5$};
\node (l23) at (1.5,-0.7) {$6$};
\node (mem) at (3,0) {Mémoire};
\node (m0) at (3,-1) {\texttt{x} $7$};
\node (m1) at (3,-1.33) {\texttt{x+2} $4$};
\node (m2) at (3,-1.66) {\texttt{x+4} $8$};
\node (m3) at (3,-2) {\texttt{x+6} $5$};
\node (m4) at (3,-2.33) {\texttt{x+8} $9$};
\node (m5) at (3,-2.66) {\texttt{x+10} $6$};
\draw [->,color=blue] (l11.west) |- (m0.west);
\draw [->,color=blue] (l12.west) |- (m2.west);
\draw [->,color=blue] (l13.west) |- (m4.west);
\draw [->,color=green] (l21.east) |- (m1.west);
\draw [->,color=green] (l22.east) |- (m3.west);
\draw [->,color=green] (l23.east) |- (m5.west);](../_images/tikz-627152bb364a103cae12e2f41b4a2ba54f25a97e.png)
Fig. 10 Stockage colonne par colonne d’une matrice
On est parfois amené à manipuler des tableaux de différentes tailles. Dans ce cas, il est intéressant de réserver un mot en mémoire pour stocker la taille du tableau. Tout tableau utilisant cette représentation contient donc comme premier élément sa taille. Un tableau de n entiers occupe donc \(n+1\) mots en mémoire.
A titre d’exemple, reprenons notre tableau avec le nombre de jours dans chaque mois. La représentation de notre tableau contient donc une entrée supplémentaire qui est sa taille (Tableau 9).
adresse |
valeur |
m |
12 |
m+2 |
31 |
m+4 |
28 |
m+6 |
31 |
m+8 |
30 |
m+10 |
31 |
m+12 |
30 |
m+14 |
31 |
m+16 |
31 |
m+18 |
30 |
m+20 |
31 |
m+22 |
30 |
m+24 |
31 |
Cette représentation a deux avantages principaux. Tout d’abord, il est possible d’écrire un programme générique qui peut parcourir tous les éléments de n’importe quel tableau comme dans l’exemple ci-dessous.
JMP start
jours: DB 0
mois:
DB 12 ; nombre d'éléments dans le tableau
DB 31
DB 28
DB 31
DB 30
DB 31
DB 30
DB 31
DB 31
DB 30
DB 31
DB 30
DB 31
start:
MOV C, 1 ; index dans le tableau
boucle:
MOV A, C
MUL 2
ADD A, mois ; adresse en mémoire du Ceme mois
MOV B, [A]
ADD B, [jours]
MOV jours, B
INC C
MOV D,[mois]
CMP C,D
JA fin
JMP boucle
fin:
HLT
De plus, lorsque cette représentation est utilisée dans un langage de programmation, celui-ci peut facilement vérifier que les accès aux éléments d’un tableau respectent bien les limites de ce tableau. C’est le cas avec le langage python.
Note
Convention de représentation des tableaux
Dans le cadre de ce syllabus, nous prendrons comme convention de représenter un tableau de n entiers comme n entiers consécutifs en mémoire mais sans indication explicite de la longueur dans le tableau lui-même. C’est la convention utilisée notamment par le langage C. Elle a l’avantage d’éviter de devoir toujours réserver un espace mémoire pour stocker la longueur du tableau alors que dans certains cas celle longueur est connue par le programme. C’était le cas notamment dans nos exemples avec les coordonnées. Dans les autres cas, la taille du tableau devra être stockée dans une autre variable qui sera elle aussi accessible au programme.
Les chaînes de caractères¶
Un programme informatique doit régulièrement utiliser des chaînes de caractères pour afficher des messages à l’utilisateur ou imprimer de l’information. Nous avons déjà vu comment représenter chaque caractère grâce à une table des caractères. Notre minuscule assembleur utilise un mot de 16 bits pour représenter chaque caractère. Une chaîne de caractères peut être vue comme un tableau de caractères. Elle sera composée de caractères consécutifs qui sont stockés en mémoire. En assembleur, nous pouvons stocker une chaîne de caractères en mémoire en utilisant directement le mot clé DB comme suit.
hello: DB "Hello World!"
Un programme devoir traiter des chaînes de caractères de tailles très différentes. Il existe deux techniques pour stocker ces chaînes de caractères en mémoire.
La première est de stocker la longueur de la chaîne suivie par les caractères qui la composent (Fig. 11). Cette solution permet de facilement déterminer la longueur de la chaîne de caractères puisque celle-ci est explicitement stockée en mémoire. En utilisant un mot de 16 bits pour cette longueur, on peut supporter des chaînes contenant au maximum 65535 caractères. C’est largement assez pour le minuscule ordinateur vu l’espace de mémoire dont il dispose.
![\node (l11) at (0,0) {H};
\node (l12) at (0.25,0) {e};
\node (l13) at (0.5,0) {l};
\node (l21) at (0.75,0) {l};
\node (l22) at (1,0) {o};
\node (l23) at (1.25,0) {!};
\node (mem) at (3,0) {Mémoire};
\node[color =red] (m) at (4,-0.66) {\texttt{a} $0000000000000111$};
\node (m0) at (4,-1) {\texttt{a+2} $00000000 01001000$};
\node (m1) at (4,-1.33) {\texttt{a+4} $00000000 01100101$};
\node (m2) at (4,-1.66) {\texttt{a+6} $00000000 01101100$};
\node (m3) at (4,-2) {\texttt{a+8} $00000000 01101100$};
\node (m4) at (4,-2.33) {\texttt{a+10} $00000000 01101111$};
\node (m5) at (4,-2.66) {\texttt{a+12} $00000000 00100001$};
\draw [->] (l11.south) |- (m0.west);
\draw [->] (l12.south) |- (m1.west);
\draw [->] (l13.south) |- (m2.west);
\draw [->] (l21.south) |- (m3.west);
\draw [->] (l22.south) |- (m4.west);
\draw [->] (l23.south) |- (m5.west);](../_images/tikz-602c34119a643cd1ae5d26805d2855aa3e162c86.png)
Fig. 11 Représentation en mémoire de la chaîne de caractères Hello! avec une indication explicite de longueur
Afin d’illustrer l’utilisation de cette représentation des chaînes des caractères, considérons un petit programme qui permet de déterminer si un caractère est présent dans une chaîne de caractères. En python, ce programme pourrait s’écrire comme suit:
mystr="Hello!"
c='h'
r=0 # absent
i=0
while(i<len(mystr)):
if mystr[i]==c:
r=1 # present
break
i=i+1
La conversion de ce programme en minuscule assembleur est présentée ci-dessous.
Notre programme a comme entrée la variable char contenant le caractère à rechercher et une chaîne de caractères qui est stockée en mémoire à partir de l’adresse correspondant à l’étiquette string`. Le résultat du programme se retrouve dans la variable ``r en mémoire.
JMP start
; Compte le nombre d'occurrences du caractère char dans la chaine string
count: DB 0
char: DB "o"
string:
DB 12 ; longueur de la chaîne
DB "Hello World!" ; Chaîne de caractères
start:
MOV C, [char] ; caractère à rechercher
MOV D, 1 ; index de la position dans la chaîne
boucle:
MOV A, D
MUL 2
ADD A, string
CMP C, [A]
JNE suite
MOV A, [count]
INC A
MOV count, A
suite:
INC D ; incrément indice boucle
MOV B, [string] ; longueur de la chaîne
CMP D, B
JBE boucle
fin:
HLT
Il existe une seconde façon de stocker les chaînes de caractères. C’est celle qui est utilisée notamment par le langage C. Ce langage utilise un caractère spécial (la valeur binaire 00000000 00000000 sur le minuscule ordinateur) pour marquer la fin de la chaîne de caractère.
![\node (l11) at (0,0) {H};
\node (l12) at (0.25,0) {e};
\node (l13) at (0.5,0) {l};
\node (l21) at (0.75,0) {l};
\node (l22) at (1,0) {o};
\node (l23) at (1.25,0) {!};
\node (mem) at (3,0) {Mémoire};
\node (m0) at (4,-1) {\texttt{a} $00000000 01001000$};
\node (m1) at (4,-1.33) {\texttt{a+2} $00000000 01100101$};
\node (m2) at (4,-1.66) {\texttt{a+4} $00000000 01101100$};
\node (m3) at (4,-2) {\texttt{a+6} $00000000 01101100$};
\node (m4) at (4,-2.33) {\texttt{a+8} $00000000 01101111$};
\node (m5) at (4,-2.66) {\texttt{a+10} $00000000 00100001$};
\node[color =red] (m6) at (4,-3) {\texttt{a+12} $00000000 00000000$};
\draw [->] (l11.south) |- (m0.west);
\draw [->] (l12.south) |- (m1.west);
\draw [->] (l13.south) |- (m2.west);
\draw [->] (l21.south) |- (m3.west);
\draw [->] (l22.south) |- (m4.west);
\draw [->] (l23.south) |- (m5.west);](../_images/tikz-350c8ae82c15b739e5046e86d6397c9e6230844a.png)
Fig. 12 Représentation en mémoire de la chaîne de caractères Hello! avec marqueur de fin
En assembleur, une telle chaîne de caractères peut être déclarée comme suit.
hello: DB "Hello!"
DB 0 ; Fin de chaîne
Avec cette représentation des chaînes de caractères, le programme ne connaît pas a priori la longueur de la chaîne de caractères. Il doit la parcourir pour trouver le marqueur de fin symbolisé par la valeur 0 (et non le caractère ASCII 0). En python, le parcours de cette chaîne peut se faire en utilisant le programme ci-dessous.
mystr="Hello!\0"
c='o'
r=0 # absent
i=0
while(mystr[i]!='\0'):
if mystr[i]==c:
r=1 # present
break
i=i+1
En assembleur, ce programme peut s’écrire comme suit.
JMP start
; Compte le nombre d'occurrences du caractère char dans la chaine string
count: DB 0
char: DB "o"
string:
DB "Hello World!" ; Chaîne de caractères
DB 0 ; Marqueur de fin de chaîne
start:
MOV C, [char] ; caractère à rechercher
MOV D, 0 ; index de la position dans la chaîne
boucle:
MOV A,D
MUL 2
ADD A, string
CMP C, [A]
JNE suite
MOV B, [count]
INC B
MOV count, B
suite:
INC D ; incrément indice boucle
MOV B, 0
CMP B, [A] ; fin de chaîne ?
JNE boucle
fin:
HLT
Note
Convention de représentation des chaînes de caractères
Dans le cadre de ce syllabus, nous prendrons comme convention de toujours représenter les chaînes de caractères avec la valeur 0x00 00 comme marqueur de fin de chaîne de caractères. C’est la convention qui est utilisée notamment par le langage C.