 |
Introduction |
|
 |
Propriétés |
 |
Fonctions trigonométriques |
 |
Fonctions trigonométriques inverses |
 |
Fonctions hyperboliques |
 |
Fonctions hyperboliques inverses |
 |
Exponentielle, logarithme et puissance |
 |
Exercices |
I.Introduction
| L'intégrale indéfinie ou primitive de f(x) sz définit ainsi |
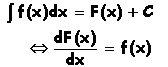 |
II.Propriétés des Intégrales
| Dans ces propriétés u et v sont des fonctions intégrables de t, a est
une constante. |
- intégrale de la somme de deux fonctions
|
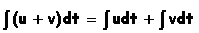 |
- intégrale d'une fonction multipliée par un scalaire
|
 |
- intégrale d'un produit de deux fonctions : une est identifiable comme primitive
|
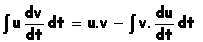 |
|
|
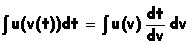 |
III.Intégrales des fonctions trigonométriques
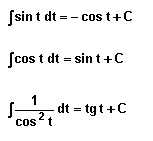
IV.Intégrales donnant fonctions trigonométriques inverses
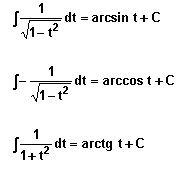
V.Intégrales des fonctions hyperboliques
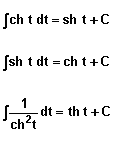
VI.Intégrales donnant des fonctions hyperboliques inverses
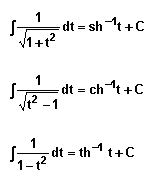
VII.Intégrales des fonctions exponentielle et de puissance
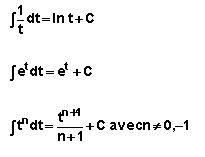
VIII.Exercices d'intégrales
On peut par exemple utiliser la boîte symbolique
associée à Matlab pour vérifier ses calculs
- définir la fonction sous forme de chaîne de caractères et la stocker dans une
variable f
f='sin(x)'
- demander de calculer la primitive de f par rapport à x et de stocker la primitive dans
une variable g
g=int(f,'x')
- demander de calculer l'intégrale de f par rapport à x dans l'intervalle [a b] et de
stocker le résultat dans une variable r
a=0
b=pi
r=int(f,'x',a,b)
Ou utiliser l'outil funtool en tapant ces
lettres comme instruction
|