 |
Définition de fonctions et représentation en mode symbolique |
|
 |
Dérivées de fonctions symboliques |
 |
Intégrales de fonctions symboliques |
I.Définition de fonctions et représentation en mode symbolique
Matlab fait la différence entre une lettre minuscule et une lettre majuscule. Toutes
les commandes et fonctions de Matlab s’écrivent en minuscules.
Pour les variables que vous utiliserez, c’est à vous à rester consistent dans votre
écriture….. bref f n’est pas F.
Les noms que vous utiliserez pour les variables sont à votre choix. Néanmoins pour plus
de clarté, n’appelez pas une variable sin, cos, …. qui sont des noms de
fonctions Matlab. Ce ne serait plus très clair pour vous également.
Fonctions courantes disponibles
Fonctions trigonométriques : ! ! les arguments sont à
exprimer en radians
sin(x), cos(x), tan(x) , asin(x), acos(x), atan(x)
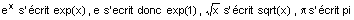
log(x) est le logarithme Népérien, log10(x) est le logarithme
en base 10
| Addition |
+ |
| Soustraction |
- |
| Multiplication |
* |
| Division |
/ |
| Exposant |
^ |
| Parenthèses de regroupement |
() |
|
|
 doit s'écrire
doit s'écrire
f = ' 2*x^2/(1+sqrt(x))'
 doit s'écrire
doit s'écrire
g = ' exp(-0.2*x)*sin(pi*x/2)'
|
|
Assignation d’une fonction symbolique à une variable
Nomdelavariable = 'expression de la fonction'
Représentation graphique d’une fonction symbolique
Pour rappel, la fonction ne doit dépendre que de UNE variable.
Soit f la fonction symbolique
ezplot( f ) représente la fonction f pour un intervalle par défaut de [ -2*pi
2*pi ]
ezplot( f , [ borneinférieure bornesupérieure ] ) représente la
fonction f pour l’intervalle précisé
Si un graphique était présent, il sera remplacé par la nouvelle fonction
Commandes supplémentaires
- Conserver les graphes de différentes fonctions dans la même fenêtre
Avant de lancer la commande du deuxième graphe, utiliser la commande hold on
- Nettoyer la fenêtre des graphiques présents
Commande clg
- Modifier les échelles du graphique a posteriori
axis( [ xinférieur xsupérieur yinférieur ysupérieur ] )
- Mettre un titre au graphique
title( ‘ titre à mettre ‘ )
- Mettre un titre aux axes
l'axe des abscisses xlabel( ' titre à mettre ' )
l'axe des ordonnées ylabel( ' titre à mettre ' )
Substitution de valeurs aux paramètres dans une fonction symbolique
Syntaxe de la fonction subs() Nomdelavariable = subs( fonctionsymbolique
, valeur ou ‘expression’, ‘paramètre’
)
f=’a*sin(2*x)’
g=subs( f , 0.5 , ‘a’ ) donne pour g ‘1/2*sin(2*x)’ …valeur
|
f2=’sin(w*x+phi)’
h=subs( f2 , 3 ,’w’ ) donne pour h ‘sin(3*x+phi)’ … valeur
h=subs( h , ‘pi/5’ , ‘phi’ ) donne pour h
‘sin(3*x+pi/5)’ … ‘expression’
v=subs( f2 , 4 ,’w’)donne pour v ‘sin(4*x+phi)’ … valeur
v=subs( v , ‘pi/2’ , ‘phi’ ) donne pour v
‘cos(4*x)’ … et oui Matlab simplifie.. |
Impression d’un graphique
- Cliquer
 dans la
fenêtre du graphique pour la rendre active dans la
fenêtre du graphique pour la rendre active
- Au menu, choisir File Print
- Vérifier que les paramètres de l’imprimante sont corrects et cliquer
 OK OK
Appel à l’aide au sein de Matlab
Si vous désirez connaître la syntaxe complète d’une commande ou d’une
fonction, tapez comme ordre :
help nom de la commande ou fonction ainsi help
ezplot
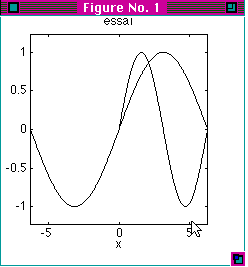
| Exemple |
Représentez la fonction sin(w x)
- dans l'intervalle 0, 2*pi pour w valant 1
- et dans l'intervalle -2pi ,2pi pour w valant 0.5 sur le même graphique.
Intitulez le graphique essai. |
La fenêtre des commandes

|
La fenêtre graphique
|
II.Dérivées de fonctions en mode symbolique
La fonction symbolique peut contenir constantes et variable.
diff(fonction à dériver , 'nom de la variable')
pour une dérivée à l'ordre 1
diff(fonction à dériver , 'nom de la
variable',ordre n) pour une dérivée à l'ordre n
f=’a*sin(2*x)’
g=diff(f,'x') donne pour g ‘2*a*cos(2*x))’ |
f=’a*sin(2*x)’
g=diff(f,'a') donne pour g ‘sin(2*x))’ |
III.Intégrales de fonctions en mode symbolique
La fonction symbolique peut contenir constantes et variable.
La primitive d'une fonction symbolique s'obtient ainsi
int(fonction à intégrer , 'nom de la variable')
!! N'oubliez pas qu'une primitive est donnée à une constante près. Des réponses
apparemment différentes peuvent donc être chacune valables. En cas de doute, dérivez
les deux résultats.
Si un intervalle est à préciser
int(fonction à intégrer , 'nom de la variable',borne
inférieure, borne supérieure)
+INF et -INF sont les représentations de l'infini
f=’a*sin(2*x)’
g=diff(f,'x') donne pour g ‘2*a*cos(2*x))’ |
f=’a*sin(2*x)’
g=diff(f,'a') donne pour g ‘sin(2*x)’ |
f=’sin(2*x)’
diff(f,'x',0,pi) donne 0 |
|