Si le rayon Ri et le rayon Re du tore sont de valeur voisines (c'est-à-dire si les dimensions des spires sont faibles devant le rayon moyen (Rm = (Ri+Re)/2)), on peut admettre, sans commettre d'erreur importante, que tous les contours d'intégration situés à l'intérieur du tore ont plus ou moins la même longueur égal à Rm.
Cette hypothèse revient à admettre que l'induction magnétique est constante en tout point d'une section droite du tore. Comme par ailleurs, l'induction ![]() est en tout point perpendiculaire à la section droite (puisque tangente au contours d'intégration), le flux y à travers une section droite du tore vaut approximativement :
est en tout point perpendiculaire à la section droite (puisque tangente au contours d'intégration), le flux y à travers une section droite du tore vaut approximativement :
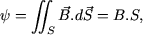
|
(4) |
En combinant (2) et (4), on calcule
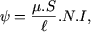
|
(5) |
 = 2.
= 2. .Rm
.Rm
On appelle :
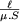 , la réluctance du circuit magnétique.
, la réluctance du circuit magnétique. ce qui permet d'écrire (5) sous la forme :
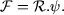
|
(6) |