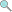4.0 credits
30.0 h + 15.0 h
1q
Teacher(s)
Ringeval Christophe ;
Language
Anglais
Main themes
Measure theory, distributions, Green's functions, spectral theory, differential forms. (Description): - Concepts of topology * Euclidian * Connected space, topological group - Measure theory and Lebesgue integral * Measurable space and functions * Lebesgue's integral * Applications to probabilities - Distributions et Green's functions * Tests functions and distributions * Operations and Fourier transforms * Green's functions * Applications to partial differential equations - Spectral theory in Hilbert's spaces * Elementary properties of Hilbert's spaces * Linear functional and operators * Spectra * Applications to polynomials and Quantum Mechanics - Concepts of differential geometry * Manifolds and differential forms * Applications to thermodynamics and Relativity
Aims
This course introduces various mathematical structures widely used in various theoretical and applied fields and necessary for the physicists. The interest of these objects will be illustrated on various concrete examples.
The contribution of this Teaching Unit to the development and command of the skills and learning outcomes of the programme(s) can be accessed at the end of this sheet, in the section entitled “Programmes/courses offering this Teaching Unit”.
Faculty or entity<