 |
Notations |
 |
Norme |
 |
Addition - Soustraction |
 |
Multiplication par un scalaire |
 |
Produit scalaire |
 |
Produit vectoriel |
|
|
I.Notations
Les vecteurs sont habituellement décrits à l'aide de leurs composantes scalaires, de
la manière suivante
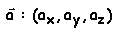
ou en utilisant les vecteurs unitaires
|
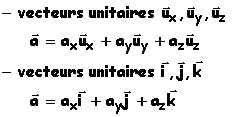 |
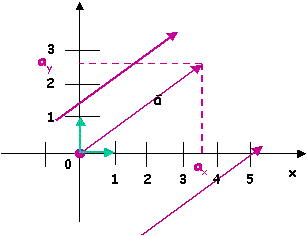
placez la souris sur la figure pour visualiser
l'animation |
ou en utilisant les coordonnées de deux points extrémités
II.Norme d'un vecteur
| La norme d'un vecteur mesure la longueur de ce dernier |
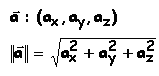 |
III.Addition - Soustraction de deux vecteurs
L'addition de deux vecteurs donne un vecteur dont les composantes
correspondent à la somme des composantes des deux vecteurs |
 |
| La différence de deux vecteurs donne un vecteur dont les composantes correspondent à
la différence des composantes des deux vecteurs |
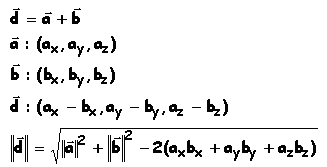 |
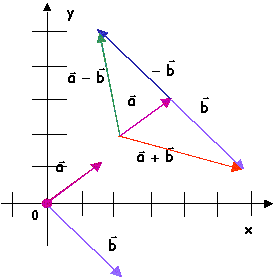
placez la souris sur la figure pour visualiser l'animation
IV. Multiplication par un scalaire
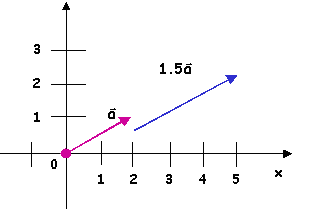
| La multiplication d'un vecteur par un scalaire donne un vecteur dont chaque composante
est multipliée par ce scalaire
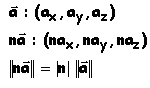
|
 |
V. Produit scalaire
Le produit scalaire de deux vecteurs est un scalaire
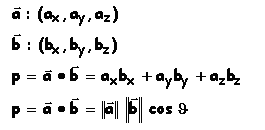
|
 |
la norme d'un vecteur est identique au produit scalaire de ce vecteur avec lui-même
le produit scalaire de deux vecteurs perpendicaulaires est donc nul
les normes de la somme et de la différence de deux vecteurs peuvent donc s'écrire
également en fonction de leur produit scalaire et de leurs normes respectives
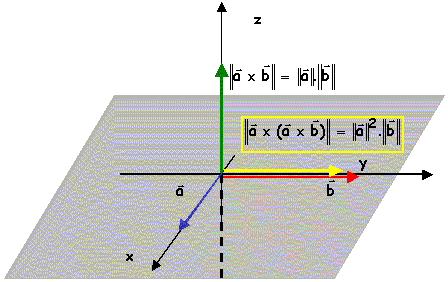
VI. Produit vectoriel
Le produit vectoriel de deux vecteurs est un vecteur dont
|
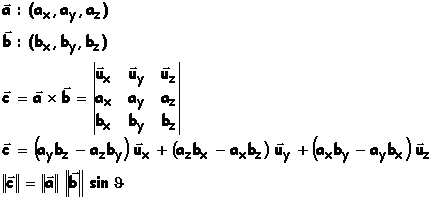 |
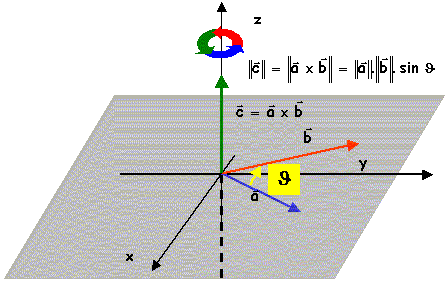
placez la souris sur la figure pour visualiser l'animation
le produit vectoriel de deux vecteurs parallèles (même sens ou sens opposé) est nul
| propriété utile :
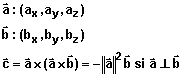
|
 |
|