 |
Equation générale |
|
 |
Méthode graphique de résolution |
 |
Outil de représentation graphique |
I. Equation générale
L'équation générale d'un courbe du second degré peut s'écrire: y=ax2+bx+c
Le calcul des racines, c'est-à-dire, des valeurs d'abscisses pour lesquelles
l'ordonnée est nulle, est généralement bien connu:
- il faut tout d'abord calculer le réalisant

- en fonction du signe du réalisant, nous obtenons des situations différentes:
- si le réalisant est strictement positif : il y a deux racines réelles distinctes (la
courbe traverse l'axe des abscisses en 2 points)
- si le réalisant est nul : il y deux racines réelles confondues (la courbe est tangente
à l'axe des abscisses)
- si le réalisant est strictement négatif : il n'y a pas de racine réelle (la valeur de
y est strictement positive ou strictement négative)
II. Méthode graphique de résolution
Une méthode graphique de résolution des racines de la courbe y=ax2+bx+c consiste à rechercher les
valeurs des abscisses des intersections de la courbe
y=x2 et de la droite y=(-bx-c)/a
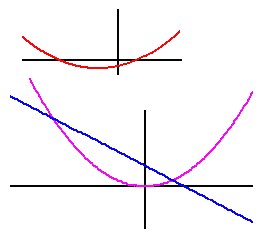 |
deux racines réelles distinctes:
la droite traverse la courbe en deux points |
 |
deux racines réelles confondues :
la droite est tangente à la courbe en un point |
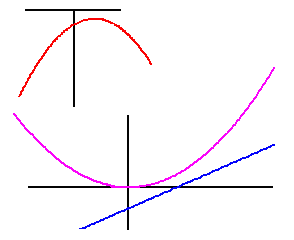 |
pas de racine réelle:
la droite ne traverse pas la courbe |
|
|
III. Outil de représentation graphique
Il suffit d'entrer les coefficients de l'équation du second degré et de presser le
bouton dessine pour obtenir les racines, visualiser la courbe du second degré et la
méthode de résolution graphique
Il a possibilité de limiter les bornes des intervalles des abscisses et/ou des
ordonnées.
|