 |
Représentation d'une grandeur sinusoïdale |
|
Représentation symbolique : nombres complexes |
|
Représentation complexe exponentielle |
|
Opérations sur les nombres complexes |
|
|
I.Représentation d'une grandeur sinusoïdale
La grandeur sinusoïdale A(t) peut se représenter comme étant la
projection sur l'axe des ordonnées d'un vecteur tournant à la vitesse angulaire w constante, dans le sens inverse aux aiguilles d'une montre, vecteur
dont la longueur vaut l'amplitude Am.
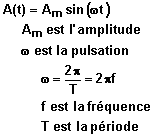
Pour t=0, le vecteur est horizontal et orienté vers la droite.
Nous noterons la représentation vectorielle de A ainsi: 
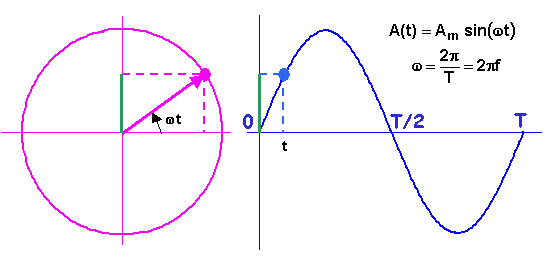
placez la souris sur le dessin pour visualiser l'animation
Si on introduit un déphasage f entre deux
sinusoïdes A(t)=Am sin(wt) et B(t)=Bm
sin(wt+f). Les deux
vecteurs tournent à la même vitesse w en conservant
leur position relative. Si f est positif, on
dira que 
est en avance de f sur ,
considéré comme référence. Si f est négatif,
on dira que
est en retard sur .
 
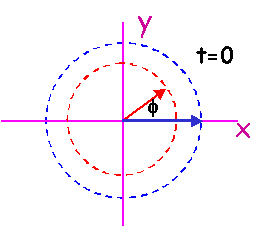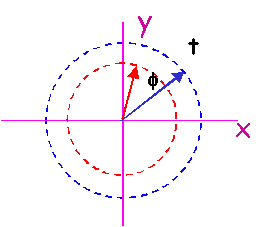
Dans la mesure où les positions relatives sont conservées (même vitesse
angulaire), on représente généralement les vecteurs tournants pour t=0
II.Représentation symbolique : nombres complexes
A partir de ce point, les sinusoïdes ont toutes la même vitesse
angulaire.
La position occupée dans le diagramme vectoriel par chaque vecteur est
caractérisée, par exemple, par ses projections sur les 2 axes perpendiculaires
(horizontal et vertical).
Nous utilisons la symbolique complexe pour représenter la grandeur
sinusoïdale A(t)=Am sin(wt+a)
en passant par l'analyse de sa représentation vectorielle pour t=0.
 |
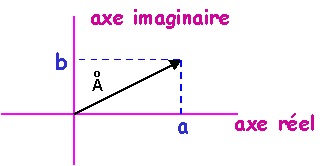la composante suivant l'axe horizontal ou réel est a
la composante suivant l'axe vertical ou imaginaire est b
le nombre complexe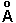
s'écrit:
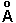= a + j b
j est l'opérateur qui "signifie" que b doit être porté sur l'axe
imaginaire |
 |
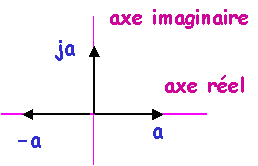Si une grandeur a est tournée de 90° vers l'avant, elle devient ja. Une
nouvelle rotation de 90° vers l'avant donnera j(ja) qui doit être
égale à -a : j*j=-1 ou encore  |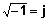
Quelques définitions
le module de
donne l'amplitude: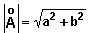 
l'argument de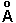
donne le déphasage: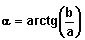 
et quelques relations: 
La représentation vectorielle est intuitive: elle permet une
représentation complexe claire de situations parfois compliquées. La représentation
complexe s'avère utile lorsqu'il s'agit de faire des calculs.
III.Représentation complexe exponentielle
A partir des développements en séries des fonctions exponentielle, sin
et cos, nous arrivons à l'expresion exponentielle des nombres complexes
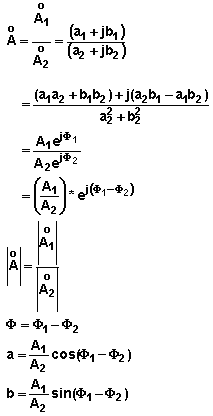
IV. Opérations sur les nombres complexes
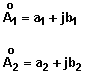 sont
les 2 nombres complexes pour lesquels les opérations d'addition, de soustraction,
de multiplication et de division vont être définies
Addition
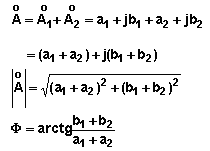
Soustraction
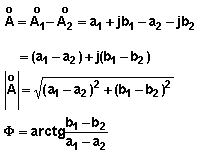
Multiplication
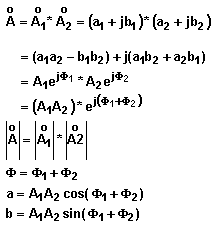
Division
| 
