 |
Arcs et Angles |
 |
Définition des fonctions trigonométriques |
 |
Relations trigonométriques |
 |
Les Triangles |
|
|
I. Arcs et Angles
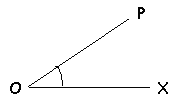 En
géométrie euclidienne, un angle plan XOP est la figure formée par deux
demi-droites issues du même point O. Le point O est appelé le sommet
de l'angle et les demi-droites ses côtés. En
géométrie euclidienne, un angle plan XOP est la figure formée par deux
demi-droites issues du même point O. Le point O est appelé le sommet
de l'angle et les demi-droites ses côtés.
Cette notion ne fait intervenir aucune idée d'orientation.
En trigonométrie et géométrie analytique, par contre, on utilise les angles
orientés. Un angle plan est considéré comme étant engendré par la rotation
dans le plan d'une demi-droite à partir de la position initiale OX jusqu'à la position
finale OP. Alors O est à nouveau le sommet, OX est appelé l'origine
et OP l'extrémité de l'angle.
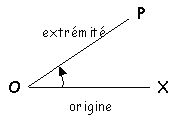
(1) |
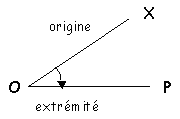
(2) |
L'angle ainsi orienté est considéré comme positif(1)
si le sens de rotation (indiqué par la flèche) est le sens contraire des aiguilles d'une
montre et comme négatif(2) si le sens de rotation est celui des
aiguilles d'une montre. |
Un degré ° est défini comme la mesure de l'angle au centre
interceptant un arc de cercle égal à 1/360 de la circonférence du cercle. Une minute
' est égale à 1/60 de degré et une seconde " vaut 1/60
de minute.
Un radian rad est défini comme la mesure de l'angle au centre
interceptant un arc de cercle égal au rayon de ce cercle. La longueur de la
circonférence d'un cercle = 2p (radians), elle corresond à un
angle de 360°.
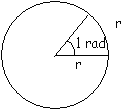
Comme 2p radians = 360°, avec p
=3.14159 on a:
1 radian = 180°/p =57.296° = 57° 17' 453
1 degré = p radian/180 = 0.017453 rad
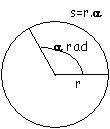 |
Soit un cercle de rayon r, un angle de a radians, au
centre, la longueur de l'arc intercepté s vaut r.a exprimé en radians |
II. Définition des fonctions trigonométriques
 |
x,y sont les coordonnées cartésiennes du point M
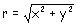 est
la norme du vecteur est
la norme du vecteur
|

Signe des nombres trigonométriques
| 2ème quadrant sin > 0
cos < 0
tg < 0
|
1er quadrant sin > 0
cos > 0
tg > 0
|
| 3ème quadrant sin < 0
cos < 0
tg > 0 |
4ème quadrant sin < 0
cos > 0
tg < 0 |
Représentation graphique des variations de fonctions trigonométriques
sin(x)
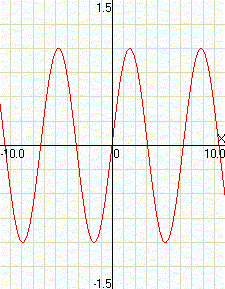
|
|
cosec(x)
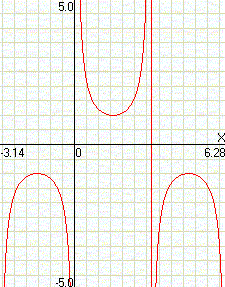
|
cos(x)
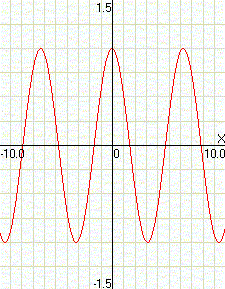
|
|
sec(x)
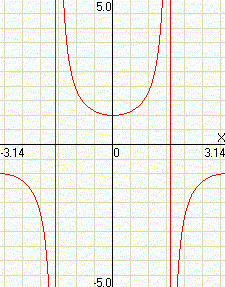
|
tg(x)
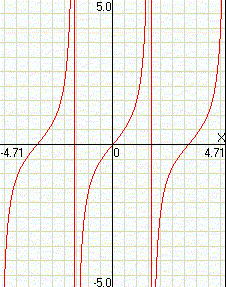
|
|
cotg(x)
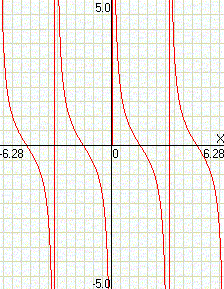
|
Pour choisir d'autres paramètres de graphiques, aller au site suivant http://www.garrinc.com/java/graph/
Valeurs pour quelques angles usuels
III.Relations trigonométriques
Relations fondamentales entre les fonctions trigonométriques d'un même arc
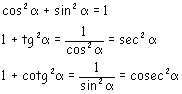
Expression de sin, cos, tg en fonction de l'une d'entre elles
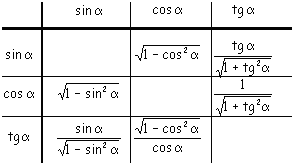 |
Ces expressions sont définies pour 0 < a < p/2
Elles restent utilisables pour d'autres valeurs de a à
condition d'ajuster les signes
|
Périodicité
| sin( a+k.2 p)=sin a |
cos( a+k.2 p)=cos a |
| tg( a+k.2 p)=tg a |
cotg( a+k.2 p)=cotg a |
|
où k est entier
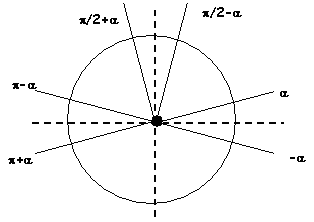
Fonctions trigonométriques de certains arcs
| sin(-a) = -sina
|
cos(-a) = cosa
|
tg(-a) = -tga |
| sin(p-a) = sina |
cos(p-a) = -cosa |
tg(p-a) = -tga
|
| sin(p+a) = -sina |
cos(p+a) = -cosa |
tg(p+a) = tga
|
| sin(p/2-a) = cosa |
cos(p/2-a) = sina |
tg(p/2-a) = cotga |
| sin(p/2+a) = cosa |
cos(p/2+a) = -sina |
tg(p/2+a) = -cotga |
|
|
|
Somme et différence de deux arcs

Mutliples d'un arc
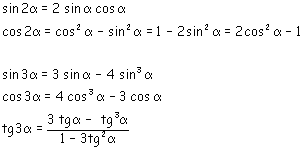
Formule de Moivre
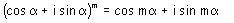
Arc double
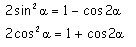
Transformations d'une somme de fonctions trigonomtriques en produit
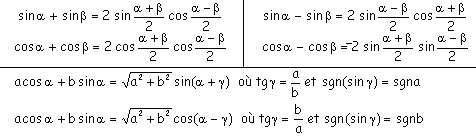
Transformations d'un produit de fonctions trigonométriques en somme
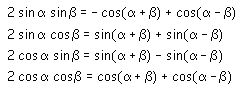
IV. Les Triangles
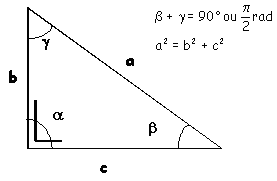 |
Considérons le traingle rectangle en a;
désignons les angles aigus par b et g
et les mesures des côtés opposés aux angles a,b,c
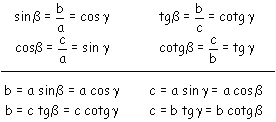
|
Quelques exercices sur les
triangles rectangles ......
Les triangles quelconques
 |
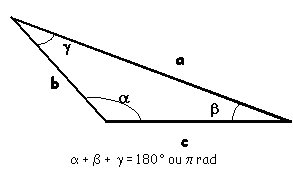 |
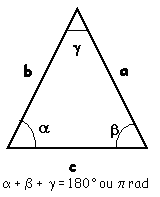
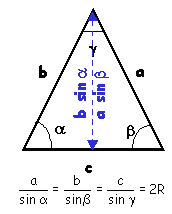
Considérons un triangle quelconque. Désignons les mesures des côtés par a,b,c, par
R le rayon du cercle circonscrit, par r le rayon du cercle inscrit et par p=(a+b+c)/2, le
demi-périmètre
|
Règle des sinus
Les côtés d'un triangle sont proportionnels aux sinus des angles opposés
Règle des cosinus
Le carré d'un côté d'un triangle est égal à la somme des carrés des deux autres
côtés diminuée du double produit de ces côtés par le cosinus de leur angle.
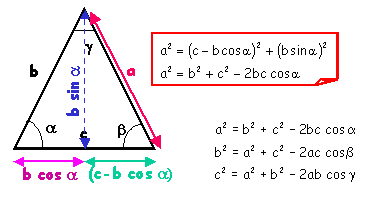
Aire d'un triangle
L'aire d'un traingle est égale au demi-produit des 2 côtés par le sinus de leur
angle
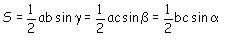
Expression des angles en fonction des côtés
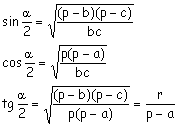
Aire d'un triangle en fonction des côtés
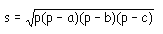
Identités usuelles
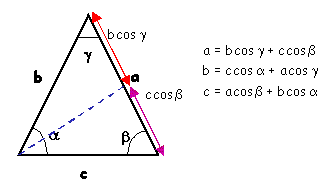
Quelques exercices sur les
triangles quelconques ......
|