|
|
Chapitre 4 :
|
Etudier un circuit linéaire en régime sinusoïdal
|
|
|
|
|
 |
Leçon 1 : Les grandeurs sinusoïdales |
 |
| |
|
Une grandeur est sinusoïdale
si elle peut s'écrire  .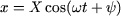
Un vecteur de norme  ,
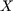faisant un angle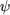 
avec l'axe horizontal en 
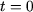et qui tourne à la vitesse 
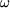dans le sens trigonométrique a une projection sur l'axe horizontal
qui vaut : .
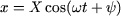Connaître le vecteur tournant équivaut donc à
connaître la grandeur sinusoïdale. Nous verrons comment,
au moyen des vecteurs tournants, additionner deux grandeurs sinusoïdales
de même pulsation, multiplier une grandeur sinusoïdale
par une constante, la dériver et l'intégrer. Enfin,
nous définirons la valeur efficace d'une grandeur sinusoÏdale. |
|
|
|
Leçon 2 : Comportement d'un circuit en régime
sinusoïdal |
|
| |
|
Nous examinerons tout d'abord
l'effet d'un courant sinusoïdal dans un élément
R, L ou C.
Nous étudierons le circuit R-L : quel est l'effet d'un courant
sinusoïdal sur une résistance et une inductance placées
en série ? A l'inverse, si une source de tension sinusoïdale
alimente une charge R-L, quelle est l'expression du courant qui va
y circuler ? L'utilisation des vecteurs tournants nous permettra de
trouver une méthode graphique et une méthode algébrique
pour résoudre ce problème.
Nous étudierons ensuite le circuit R-C, qui comporte une résistance
et une capacité placées en série.
Nous étenderons les méthodes de résolution vues
dans ces deux premiers cas à l'étude de circuits plus
complexes. |
|
|
|
| |
Leçon 3 : La méthode des phaseurs |
|
| |
|
On peut exprimer un vecteur tournant
comme un nombre complexe dont la partie réelle est la grandeur
sinusoïdale associée. Nous définirons : le substitut
complexe d'une grandeur sinusoïdale, la notion de phaseur. Nous
verrons comment effectuer les opérations (addition, multiplication,
dérivation, intégration) sur les grandeurs sinusoïdale
au moyen des phaseurs.
Nous exprimerons les liaisons entre courant et tension dans les éléments
R, L, C cette fois en terme de phaseurs, aboutirons à la loi
d'Ohm généralisée et définirons la notion
d'impédance.
Si on effectue la résolution d'un circuit par les phaseurs, on obtient
un ensemble d'équations algébriques similaires à
celles d'un circuit à courant continu ne comportant que des
résistances, mais ces équations sont des équations
sur des grandeurs complexes. On peut donc utiliser les mêmes
techniques de résolution : mise en série et en parallèle,
dipôle de Thévenin et principe de superposition (s'il
y a plusieurs sources). |
|
|
|
|
