 |
 |
Chapitre 4 : Etudier un circuit linéaire en régime sinusoïdal - notions théoriques
|
||||
|
|
||||
 |
Cours 1 : Le substitut complexe d'une grandeur sinusoïdale | |||
 |
||||
| On peut exprimer un vecteur tournant comme un nombre complexe dont la partie réelle est la grandeur sinusoïdale associée. Nous définirons : le substitut complexe d'une grandeur sinusoïdale, la notion de phaseur. Les phaseurs permettent d'effectuer les opérations (addition, multiplication, dérivation, intégration) sur les grandeurs sinusoïdale. | ||||
|
|
||||
|
Cours 2 : Les impédances | |||
|
||||
Retour à l'étude des circuits
: nous exprimerons les liaisons entre courant et tension dans les
éléments R, L, C, cette fois en terme de phaseurs. Les relations sont
toutes de la forme  :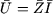
c'est la loi d'Ohm généralisée. La grandeur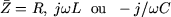 
est appelée l'impédance. |
||||
|
|
||||
| |
Cours 3 : Résolution d'un circuit par les phaseurs | |||
|
||||
| Enfin, nous effectuerons la résolution
d'un circuit par les phaseurs. Comme on conserve les lois de Kirchhoff et que les équations aux bornes des éléments sont toutes de la forme ,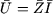
on obtient un ensemble d'équations algébriques similaires
à celles d'un circuit à courant continu ne comportant
que des résistances, mais ces équations sont des équations
sur des grandeurs complexes. On utilisera donc les mêmes techniques
de résolution : mise en série et en parallèle,
dipôle de Thévenin et principe de superposition (s'il
y a plusieurs sources). |
||||
|
|
||||
|
|
