| Ecrire et résoudre les équations
d'un circuit linéaire ... |
|
|
|
 |
Leçon 1 : qui comporte une source
et des résistances |
 |
| |
|
Nous définirons tout d'abord la méthode
générale de résolution d'un circuit : les lois
de Kirchhoff et les équations des éléments nous
fournissent le nombre d'équations nécessaires pour calculer
tous les courants et toutes les tensions du circuit. Nous verrons
comment simplifier le calcul, soit par la mise en série et
en parallèle, soit en utilisant le dipôle de Thévenin
(de Norton). Enfin, nous étudierons quelques cas particuliers
intéressants, pour lesquels la résolution est quasi
immédiate. |
|
|
|
Leçon 2 : qui comporte plusieurs sources et
des résistances |
|
| |
|
Nous étendrons les méthodes vues dans
la leçon précédente (méthode générale,
mise en série et en parallèle, dipôle de Thévenin)
au cas où il y a plusieurs sources. Nous définirons
et appliquerons le principe de superposition. |
|
|
| |
Leçon 3 : qui comporte une inductance ou une
capacité |
|
| |
|
Après un bref rappel des propriétés
de l'inductance (ou de la capacité), nous expliciterons comment
écrire et résoudre les équations du circuit :
par la méthode générale, en utilisant la mise
en série et en parallèle, en utilisant le dipôle
de Thévenin.
Nous examinerons ensuite comment comprendre et interpréter
la solution, dans le cas où la source de tension est une source
continue, et dans le cas où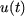 
est une fonction sinusoïdale.
Enfin, nous examinerons le cas où il y a des interrupteurs. |
|
|
 |
Leçon 4 : qui comporte plusieurs inductances
et/ou capacités |
|
| |
|
 |
| |
|
|
|
|
