 |
 |
Chapitre
3
: Ecrire et
résoudre les équations d'un circuit linéaire - Notions
théoriques
Leçon
3 : comportant une inductance ou une
capacité
|
||||
|
|
||||
 |
Cours 1 : Comment écrire et résoudre les équations ? | |||
 |
||||
Dans ce premier cours, nous verrons
comment écrire et résoudre les équations d'un
circuit comportant une inductance : par la méthode générale,
en utilisant la mise en série et la mise en parallèle,
en utilisant le dipôle de Thévenin (de Norton). Nous
obtenons une équation différentielle du premier ordre,
dont la variable est le courant dans l'inductance  .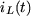
Pour résoudre cette équation différentielle,
il faut connaître l'expression de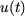 
et la valeur 
à l'instant (généralement zéro) à
partir duquel on veut connaître la réponse. Nous calculerons
la réponse dans le cas où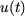
est une fonction continue et dans le cas où la tension
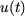est une fonction sinusoïdale. Une fois
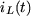connu, on peut obtenir les courants et les tensions du circuit. |
||||
|
Cours 2 : Comprendre et interpréter la solution | |||
|
||||
| Pour les deux cas que nous avons résolu
(source de tension continue et source de tension sinusoïdale),
nous allons tenter de comprendre et interpréter la solution
que nous avons obtenue en résolvant l'équation différentielle.
Dans le cas de la source de tension continue, nous développerons quelques astuces pour se faire une idée de la solution sans faire un calcul complet, et examinerons le cas de plusieurs sources. |
||||
|
Cours 3 : Que faut-il faire s'il y a des interrupteurs ? | |||
|
||||
| Si le circuit que nous avons étudié comporte deux interrupteurs, qui s'ouvrent et se ferment en des instants donnés, comment les courants et tensions du circuit vont-ils évoluer au cours du temps ? | ||||
 |
Cours 4 : Quelques cas particuliers | |||
|
||||
 |
||||
|
|
||||
|
|
