Chapitre
: Principes de fonctionnement des machines polyphasées à champ
tournant
Laboratoire :
Réalisation d'un enroulement réparti assurant une répartition
quasi sinusoidale du champ dans l'entrefer
Enoncé du laboratoire
| 1. |
|
|
|
Réponse |
|||
|
|
|||
| 2. |
Calculer les coefficients de Fourier des harmoniques d'espace de ce champ et tracer son spectre. |
||
Réponse |
|||
|
|
|||
| 3. |
Effectuez le même calcul pour une bobine |
||
Réponse |
|||
|
|
|||
| 4. |
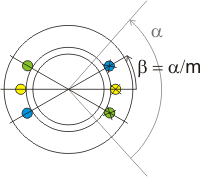
On considère un enroulement
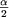 ) , connectées en série et donc parcourues
par le même courant I. La figure 2 représente un tel enroulement
dans le cas où N=2. ) , connectées en série et donc parcourues
par le même courant I. La figure 2 représente un tel enroulement
dans le cas où N=2. |
||
|
|
|||
a) Quel est le champ H créé par cet enroulement ? |
|||
Réponse |
|||
b) Calculer les coefficients de Fourier des harmoniques d'espace correspondant. |
|||
Réponse |
|||
c) Quel angle d'étalement a permet l'annulation de l'harmonique 3 du champ? Quel angle a permet l'annulation de son harmonique 5? |
|||
Réponse |
|||
|
|
|||
| 5. |
|
|
|
Réponse |
|||
|
|
|||
| 6. |
|
||
Réponse |
|||

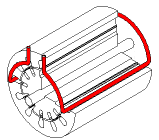
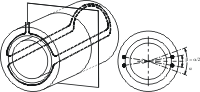
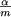 ) (cf. Figure 3).
) (cf. Figure 3).