Question 3 : démonstration
| On se base sur le schéma équivalent d'une phase (figure 1). |
|
|
| |
Comme l'induit est mis en court-circuit on a 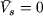 et donc : et donc :
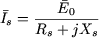
soit en module
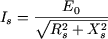
Pour une valeur donnée de 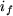 , par exemple , par exemple 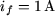 , on a : , on a :
- à partir de l'essai à vide
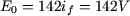
- à partir de l'essai en court-circuit

D'où

L'augmentation de la puissance mécanique fournie par le moteur d'entraînement lorsque 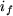 passe de zéro à 1,23 A correspond aux pertes Joule dues aux courants circulant dans les enroulements de l'induit dans le second cas. En effet comme : passe de zéro à 1,23 A correspond aux pertes Joule dues aux courants circulant dans les enroulements de l'induit dans le second cas. En effet comme :
- les pertes mécaniques restent constantes puisqu'on tourne à vitesse constante;
- on peut négliger les pertes magnétiques puisque la machine est en court-circuit et travaille à flux total virtuellement nul;
- la puissance consommée par le circuit inducteur provient de la source qui l'alimente.
l'augmentation de puissance consommée ne peut donc correspondre qu'aux pertes Joule dues aux courants d'induit. On peut écrire :

D'où

On a :
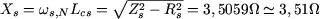
On peut vérifier que la valeur de 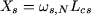 est quasiment égale à celle qu'on obtiendrait en négligeant est quasiment égale à celle qu'on obtiendrait en négligeant  dans le schéma de la figure 1 et en écrivant (figure 2) : dans le schéma de la figure 1 et en écrivant (figure 2) :
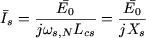
|

Figure 2
|
|
|
pour 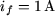 par exemple, on a par exemple, on a  , , 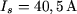 , d'où : , d'où :
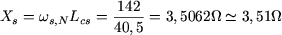
Remarque : on peut également calculer  et et 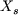 en calculant le en calculant le 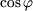 . Pour . Pour 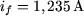 , on a : , on a :
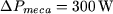


D'où :
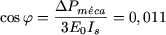
Le courant 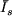 est diphasé de -89,34° en arrière par rapport à est diphasé de -89,34° en arrière par rapport à 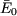 . L'argument y de l'impédance . L'argument y de l'impédance 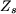 est donc de 89,34°. D'où : est donc de 89,34°. D'où :
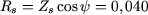
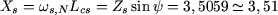
| |
| | © e-lee.net