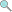Introduction à l'analyse

• understanding of mathematical tools and techniques based on a rigorous learning of concepts favored by highlighting their practical application,
• careful handling of these tools and techniques in the framework of applications.

• sets (intersection, union, difference)
• Order and equivalence,
• Interval, upper bounds, lower bounds, extremes,
• absolute value, powers and roots
• sequence of numbers and recurrence equation

Real functions of one variable

• injective, surjective, bijective functions,
• algebraic operations on functions (including graphic interpretation)
• first order functions,
• exponential, logarithmic and trigonometric functions
• Composition of functions and inverse functions

• conditions to ensure that a limit exists,
• limits to infinity

continuous functions

• fundamental theorems of continuous functions,

differentiable functions

• derivative at a point (including graphical interpretation)
• The Hospital's theorem,
• linear approximation of a function,
• maximum and minimum,
• encreasing of decreasing function (sign study)
• concavity and convexity,
• asymptotes,

• primitive,
• definite integrals (including graphic interpretation)
• undefinite integrals

Given the learning outcomes of the "Bachelor in Engineering" program, this course contributes to the development, acquisition and evaluation of the following learning outcomes:

• S1.G1
• S2.2

Students completing successfully this course will be able to

• Model real problems using the concepts of set, function, limit, derivative and integral;
• Solve real problems using computational techniques for limit, derivative and integral;;
• Reason using correctly the mathematical notations and  methods keeping in mind but exceeding a more intuitive understanding of the concepts.

The contribution of this Teaching Unit to the development and command of the skills and learning outcomes of the programme(s) can be accessed at the end of this sheet, in the section entitled “Programmes/courses offering this Teaching Unit”.