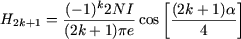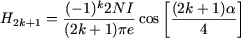Chapitre
: Principes de fonctionnement des machines polyphasées à champ
tournant
Laboratoire :
Réalisation d'un enroulement réparti assurant une répartition
quasi sinusoidale du champ dans l'entrefer
Question 4b : démonstration
|
Là encore deux approches sont possibles : |
||
|
|
||
|
|
||
|
De même que précédemment,
on calcule, compte-tenu de la forme du
champ : 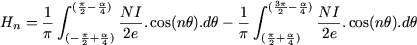
Deux cas se présentent encore :
|
||
|
|
||
|
|
||
|
L'harmonique de rang n du champ créé par deux bobines est égal à la somme des harmoniques de même rang des champs créés par chacune des deux bobines; comme le champ H est une fonction paire, on a :

où (pour i = 1 ou i = 2) : 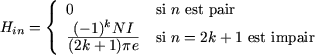
On en déduit immédiatement que les harmoniques Hn de rang pairs sont nuls. Comme pour q = 0, on a :
On en déduit que les coefficients de Fourier des harmoniques de rang impairs sont égaux à :
|
||
|
Construction géométrique du coefficient Hn L'équation (1) donne lieu à une interprétation géométrique immédiate qui permet de déterminer la valeur du coefficient Hn : |
||
|
|

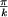 . L'intégrale de cette fonction calculée entre
. L'intégrale de cette fonction calculée entre
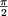 +
+