 |
 |
Chapitre
: Principes de fonctionnement des machines polyphasées à champ
tournant
Laboratoire :
Réalisation d'un enroulement réparti assurant une répartition
quasi sinusoidale du champ dans l'entrefer
Question 3 : vérification
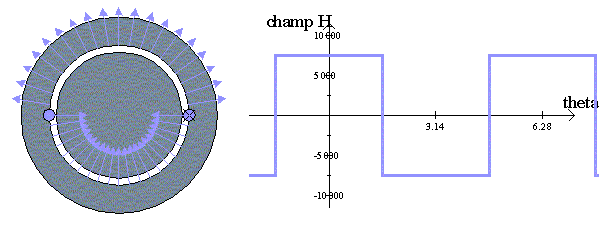
| On peut vérifier la pertinence des hypothèses posées pour le calcul théorique en comparant les résultats ainsi obtenus (figure 1) avec ceux donnés par une modélisation par éléments finis. | |
|
|
|
| Cette technique de calcul permet de résoudre numériquement les équations locales du champ dans la machine. Elle est basée sur une discrétisation de l'espace permettant l'intégration numérique des équations de Maxwell. | |
|
|
|
|
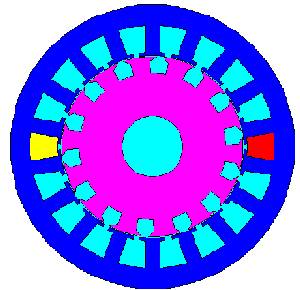
On considère la machine dont une coupe est représentée sur la figure 2. Les surfaces en bleu et en magenta correspondent respectivement aux tôles du stator et du rotor. Ces tôles sont constituées d'un matériau ferromagnétique dont la perméabilité relative est élevée tant que le champ n'a pas atteint le niveau de saturation. Les zones représentées en bleu turquoise correspondent à des zones ayant toutes d'un point de vue magnétique, les mêmes propriétés que celles l'air. Elles peuvent correspondre soit effectivement à de l'air (dans l'entrefer notamment), soit à des conducteurs en cuivre dans lesquels ne passerait aucun courant (cas des encoches du rotor et de la plupart des encoches du stator) ou encore de l'axe du motor (que l'on a supposé ici en acier amagnétique). Enfin, les deux surfaces en rouge et en jaune correspondent aux deux encoches contenant des conducteurs parcourus par un courant non nul. |
On ne considérera pas dans cette étude chacun
de ces conducteurs, sa section et sa position exacte (que l'on serait
d'ailleurs incapables de déterminer avec précision compte-tenu des
aléas introduits par le procédé de bobinage) mais on assimilera plutôt
ces deux encoches à des zones contenant un matériau dont les caractéristiques
magnétiques sont celles de l'air et parcourues par une densité de
courant j constante et égale à  où N est le nombre
de spires de la bobine, I le courant qui y circule, S
la surface de l'encoche et k le coefficient de remplissage,
à savoir le rapport entre la surface total des conducteurs et celle
de l'encoche (k =  si on désigne par  c la section d'un conducteur).
|
|
|
|
La surface d'étude a été
divisée en environ 6000 éléments dont la forme
doit être, pour avoir un bon maillage de l'espace, la plus proche
possible de celle d'un triangle équilatéral. Le maillage
est plus serré aux environs de l'entrefer (figure 3) et plus
lâche ailleurs (comme par exemple au niveau de l'axe ou sur
les parties extérieures du stator) pour limiter le nombre d'éléments.
A ces éléments sont associés environ 12000 points
(les noeuds) correspondant soit aux sommets des ces triangles, soit
aux centres de leurs cotés. C'est en chacun de ces points qu'est
calculé le potentiel vecteur 
(défini par  = 
), qui pour un problème à deux dimensions comme celui-ci
n'a qu'une composante non nulle, sa composante A z orthogonale au plan de la figure.
|
|
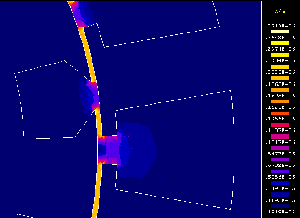
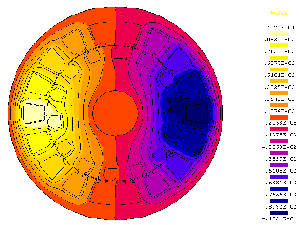
La figure 4 représente la valeur de ce potentiel vecteur en tout point de la machine. On constate qu'il est négatif autour de l'encoche contenant des conducteurs parcourus par des courants entrant dans le plan de la figure et positif autour de l'autre encoche. Les lignes d'isovaleurs du potentiel vecteur correspondent aux trajectoires suivies par le flux magnétique. On constate bien que ce flux entoure les deux encoches. |
|
Si on observe
maintenant les valeurs du champ H, on voit sur la figure 5 que sa
norme est quasi nulle partout sauf dans l'entrefer. |
|
|
|
|
|
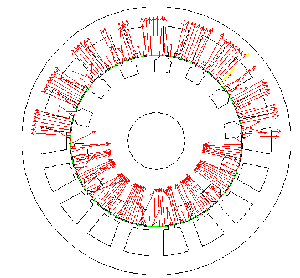
Sur la figure 6, on a représenté enfin sous forme vectorielle, le champ H calculé en tout point d'un cercle situé au milieu de l'entrefer. On constate que cette représentation est assez proche de celle obtenue par le calcul analytique précédent (figure 1). Les seules différences proviennent de la présence des encoches tant au rotor qu'au stator qui déforment localement le champ. |
|
|
