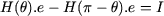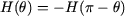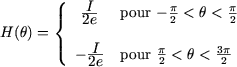Chapitre
: Principes de fonctionnement des machines polyphasées à
champ tournant
Laboratoire
: Réalisation d'un enroulement réparti assurant une répartition
quasi sinusoidale du champ dans l'entrefer
Question 1 : démonstration
|
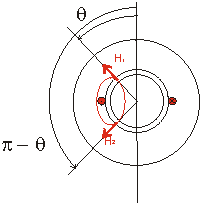
Pour calculer le champ H en un point M de l'entrefer de position angulaire q, il suffit d'appliquer le théorème d'Ampère à un contour G, traversant l'entrefer respectivement en q et p-q (cf. Figure 1). On a alors :
| |||||
|
Comme on suppose la perméabilité du fer infinie, le champ H est nul dans le fer (on a en effet H = B / m), les seules portions du contour G qui nous intéressent sont donc les traversées de l'entrefer. | |||||
|
Comme l'entrefer est mince, on peut admettre que le champ y est
purement radial. Pour un courant I positif, le champ est
positif (se dirige du rotor vers le stator) pour |
|||||
L'équation (1) devient alors :
De plus, par raison de symétrie, la valeur du champ H en q est égal à l'opposée de celle du champ H en p - q.
|
|||||
|
On en déduit finalement :
| |||||

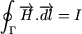
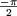 < q <
< q < 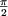 et négatif (se dirige du stator vers le rotor)
pour
et négatif (se dirige du stator vers le rotor)
pour 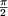 < q <
< q < 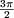 .
.