Théorème de Gauss 2

Application du théorème de Gauss pour le calcul du champ électrique: exemple 2

Même distribution que l'exemple 1, mais on veut calculer le champ en un point à l'intérieur de la sphère.

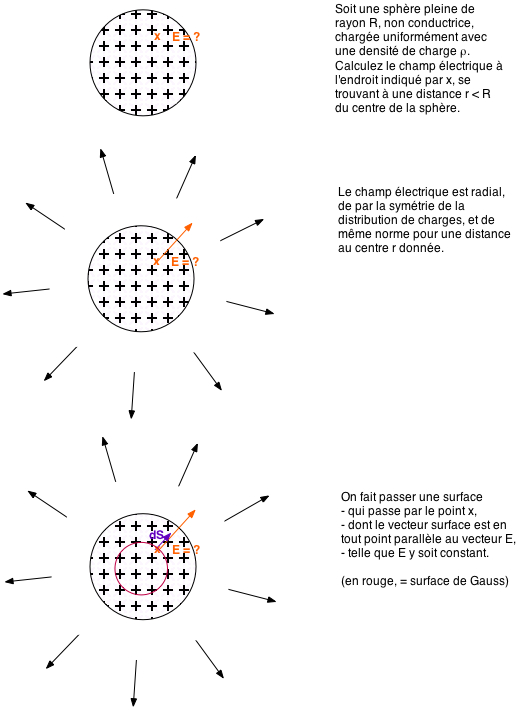
• Ecrire le théorème de Gauss: ∫ £E . d£S = Q_int / ε₀
  
  
• Détailler le membre de gauche: l'intégrale sur toute la surface peut être décomposée en somme d'intégrales sur différentes zones de cette surface. L'intérêt est de parvenir à ce que sur chaque zone, l'angle entre E et dS soit constant ainsi que la norme de E ==> On peut faire sortir E_i . cosθ_i de l'intégrale, et ∫ dS_i = S_i.
  ∫ £E . d£S = ∫ E . dS . cos0° = ∫ E . dS = E . ∫ dS = E . S = E . 4 . π . r²
  
  
• Détailler le membre de droite: on compte toutes les charges se trouvant à l'intérieur de la surface de Gauss (et seulement celles-là).
  Q_int / ε₀ = ∫ ρ . dV / ε₀ = ρ . 4/3 . π . r³ / ε₀
  
  
• En appliquant l'égalité, on peut isoler et calculer E.
  E . 4 . π . r² = ρ . 4/3 . π . r³ / ε₀ ==> E = 1/3 . ρ . r / ε₀