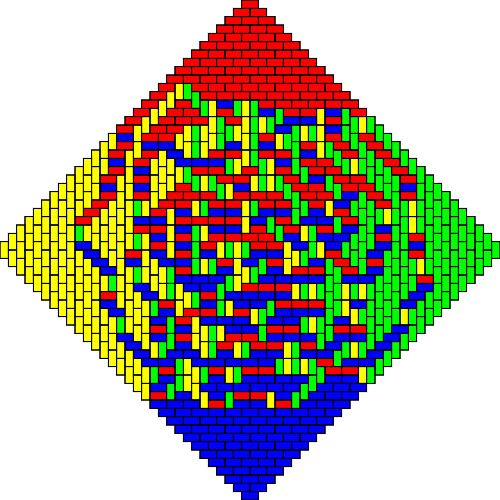
The first example is the tiling of an Aztec Diamond of order 30. The *order* of a Diamond represents the number of rows in the upper half part of the region.
The tiling is drawn uniformly at random. That means that, among all the possible tilings of the Aztec Diamond of order 30, we took one at random, with each of them having equal probability of being picked.
Although there are only two types of dominoes (horizontal and vertical dominoes), we paint the dominoes with four colours, two colours for each type. These four types of dominoes may seem artificial, but they come very naturally in the study of Aztec Diamonds. A more precise explanation can be found below.

The second is an example of the tiling of a 40 by 30 rectangle. It is drawn uniformly among all the tilings of such a rectangle.
Although apparently much simpler than the Aztec Diamond, the formula giving the number of tilings is much more complicated.

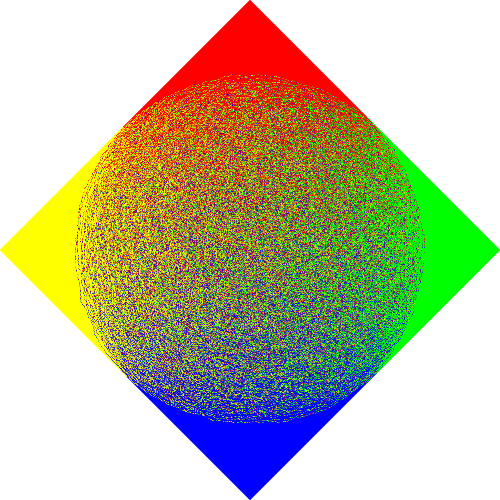
Next is an Aztec Diamond of order 1000 drawn uniformly. The number of such diamonds is way bigger than the number of particles in the universe. Yet, the algorithm is able to generate one uniformly at random, by reducing the problem to generating (a reasonable amount of) Bernoulli independent random variables.
If these Bernoulli's are independent, it is proven that the result of the algorithm is a random tiling drawn uniformly. You just need to trust that your computer is capable of that.

In the picture, we can witness the phenomenon of the Arctic Circle. The dominoes outside of the inscribed circle are frozen into only one of the four types of dominoes.

Another way to tile a region of the plane is by using lozenges. On the left, we generated a random tiling of a hexagon, tiled with three types of lozenges.
By colouring two types in white, and the last in black, we see that it can be put in relation with little cubes that we put in the corner of a cubic room.

The algorithm for generating Aztec diamonds may surprisingly be used to generate lozenge tilings. The three types of lozenges are mapped to three of the four types of dominoes, and we forbid the last type to appear.