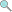5.0 credits
30.0 h + 22.5 h
2q
Teacher(s)
Papavasiliou Anthony ;
Language
Anglais
Prerequisites
- Fluency in English at the level of course LANGL1330
- Linear programming , integer programming
- Familiarity with probability theory
- Familiarity with math programming languages (AMPL, Mosel)
Main themes
- Mathematical background (duality, KKT optimality conditions, monotone operators)
- Mathematical programming models and languages
- Applications: finance, logistics, risk management, energy
Aims
In reference to the AA standard, this course contributes to the development, acquisition and evaluation of the following learning outcomes:
- AA1.1, AA1.2, AA1.3
- AA2.2, AA2.5
At the end of the course, students will be able to:
- Formulate problems of decision-making under uncertainty as mathematical programs
- Identify structure in large-scale mathematical programs that enables their decomposition
- Design algorithms for solving large-scale optimization problems under uncertainty
- Implement algorithms for solving large-scale optmization problems in AMPL
- Evaluate the quality of policies for making decisions under uncertainty
The contribution of this Teaching Unit to the development and command of the skills and learning outcomes of the programme(s) can be accessed at the end of this sheet, in the section entitled “Programmes/courses offering this Teaching Unit”.
Evaluation methods
- Written exam
- Course project and regular homework assignments
Teaching methods
2 hours of magistral courses per week, and 2 hours of training sessions per week. Homeworks and term projects will be evaluated by the instructor and/or the teaching assistant.
Content
- Stochastic programming models
- Value of perfect information and the value of the stochastic solution
- The L-shaped method in two and multiple stages
- Multi-cut L-shaped algorithm
- Stochastic dual dynamic programming
- Scenario selection and importance sampling
- Lagrangian relaxation
- Stochastic integer programming
- Monotone operators, proximal point algorithms and progressive hedging
Bibliography
- Course notes
- Printouts from textbooks or archived journals will be provided during lectures. The following textbook will be followed closely for most of the course: John Birge, Francois Louveaux, "Introduction to Stochastic Programming"
Faculty or entity<